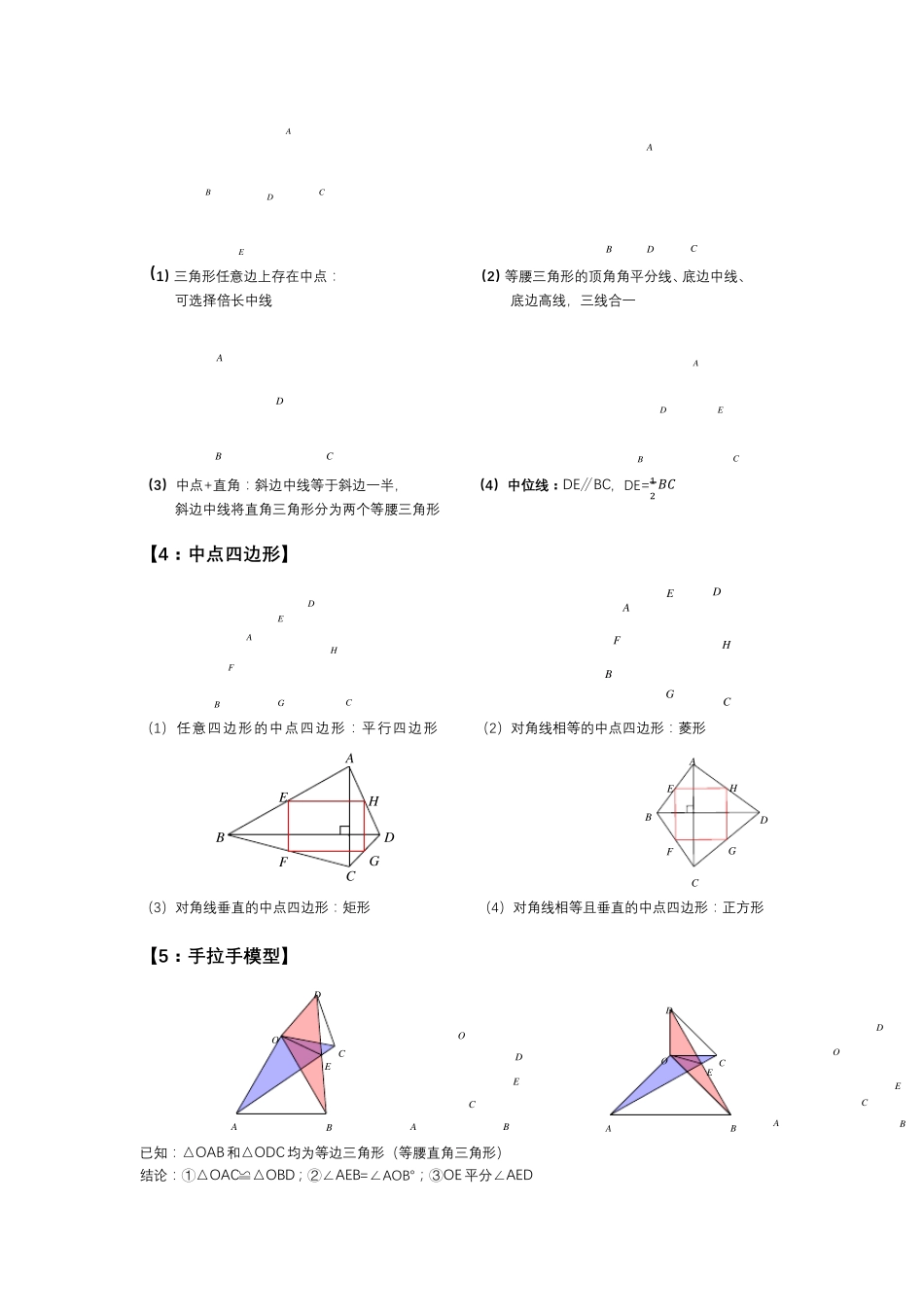
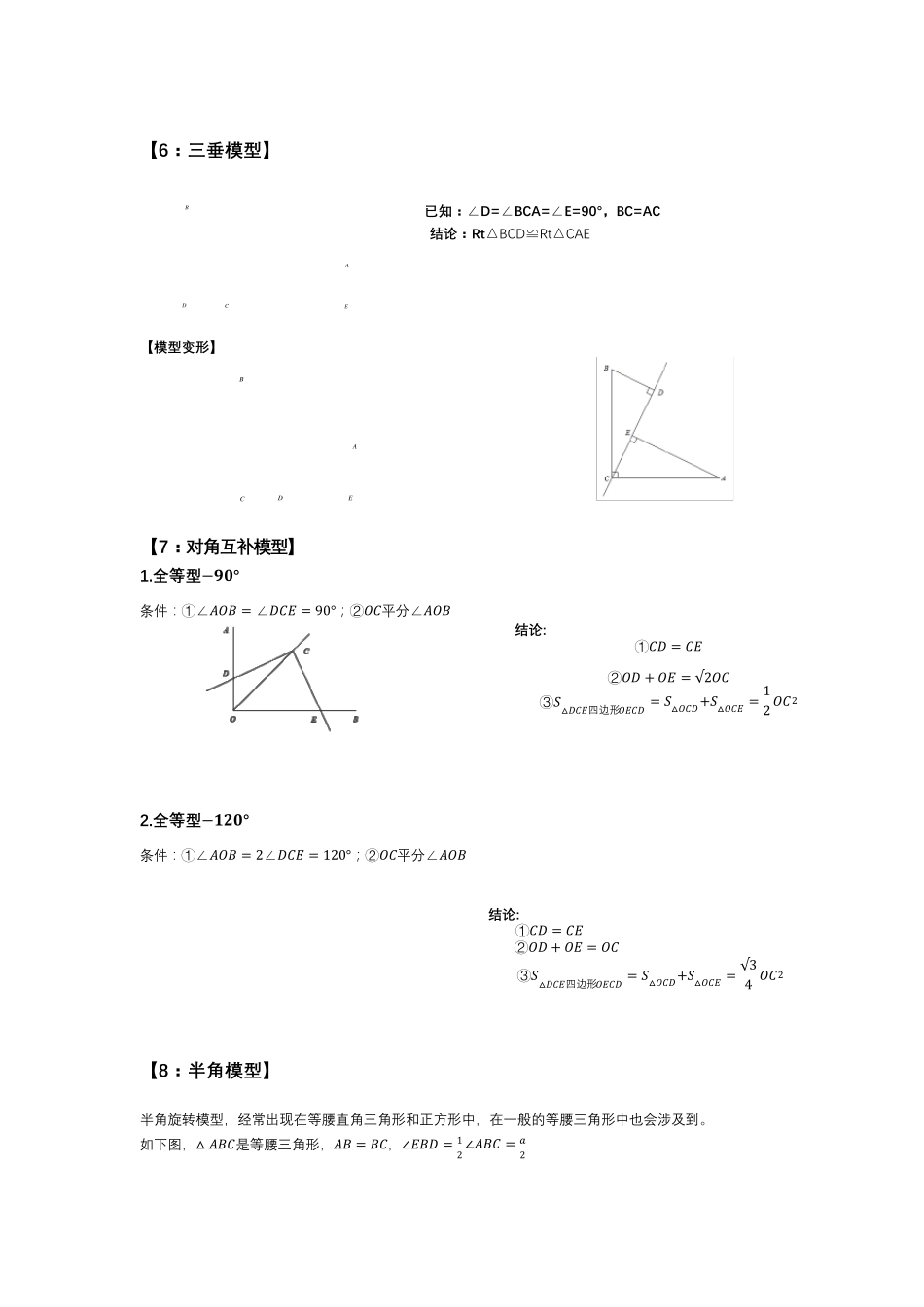
初 中 几 何 模 型 【 1: 角 平 分 线 模 型 】 ( 1) 内 内 模 型 ( 2) 内 外 模 型 1902PA 12PA ( 3) 外 外 模 型 ( 4) 双 角 平 分 线 1902PA 2ACP 【 2: 角 平 分 线 辅 助 线 】 ( 1) 向 两 边 做 垂 线 ( 2) 延 长 — — 胆 大 包 天 △ CDO≌ △ CEO △ CDO≌ △ CEO ∴ OD=OE ∴ OD=OE ( 3) 截 取 — — 任 意 情 况 ( 4) 黄 金 搭 档 △ CDO≌ △ CEO ∠ 1=∠ 2, ∠ 2=∠ 3 ∴ CD=CE ∴ OD=CD 【 3: 四 大 中 点 辅 助 线 】 ABCPDABCPFEABCPPCDBAO ( 1) 三角形任意边上存在中点: ( 2)等腰三角形的顶角角平分线、底边中线、 可选择倍长中线 底边高线,三线合一 ( 3) 中点+直角:斜边中线等于斜边一半, ( 4) 中 位 线 : DE∥BC,DE=12 ᵃᵃ 斜边中线将直角三角形分为两个等腰三角形 【 4: 中 点 四 边 形 】 (1)任意四边形的中点四边形:平行四边形 (2)对角线相等的中点四边形:菱形 (3)对角线垂直的中点四边形:矩形 (4)对角线相等且垂直的中点四边形:正方形 【 5: 手 拉 手 模 型 】 已知:△OAB和△ODC均为等边三角形(等腰直角三角形) 结论:①△OAC≌△OBD;②∠AEB=∠AOB°;③ OE 平分∠AED CDEBACDBADCBACBEDAHGFEDCBAHGFEDCABHGFEDCBAABCDEFGHEDOCBAABECODABOCEDDECOBA 【6:三垂模型】 已知:∠D=∠BCA=∠E=90°, BC=AC 结 论 :Rt△ BCD≌ Rt△ CAE 【模型变 形 】 【7:对 角 互 补 模型】 1.全 等 型−ᵽᵼ° 条 件 : ① ∠ ᵃᵄᵃ = ∠ ᵃᵃᵃ = 90°; ② ᵄᵃ平 分 ∠ ᵃᵄᵃ 2.全 等 型−ᵼᵽᵼ° 条 件 : ① ∠ ᵃᵄᵃ = 2∠ ᵃᵃᵃ = 120°; ② ᵄᵃ平 分 ∠ ᵃᵄᵃ 结 论 : ① ᵃᵃ = ᵃᵃ ② ᵄᵃ + ᵄᵃ = ᵄᵃ ③ ᵄ△ᵃᵃᵃ四 边 形 ᵄᵃᵃᵃ = ᵄ△ᵄᵃᵃ+ᵄ△ᵄᵃᵃ = √34 ᵄᵃ2 【8:半 角 模型】 半 角 旋 转 模 型 , 经 常 出 现 在 等 腰 直 角 三 角 形 和 正 方 形 中 , 在 一 般 的 等 腰 三 角 形 中 也 会 涉 及 到 。 如 下 图 , △ ᵃᵃᵃ是 等 腰 三 角 形 , ᵃᵃ...