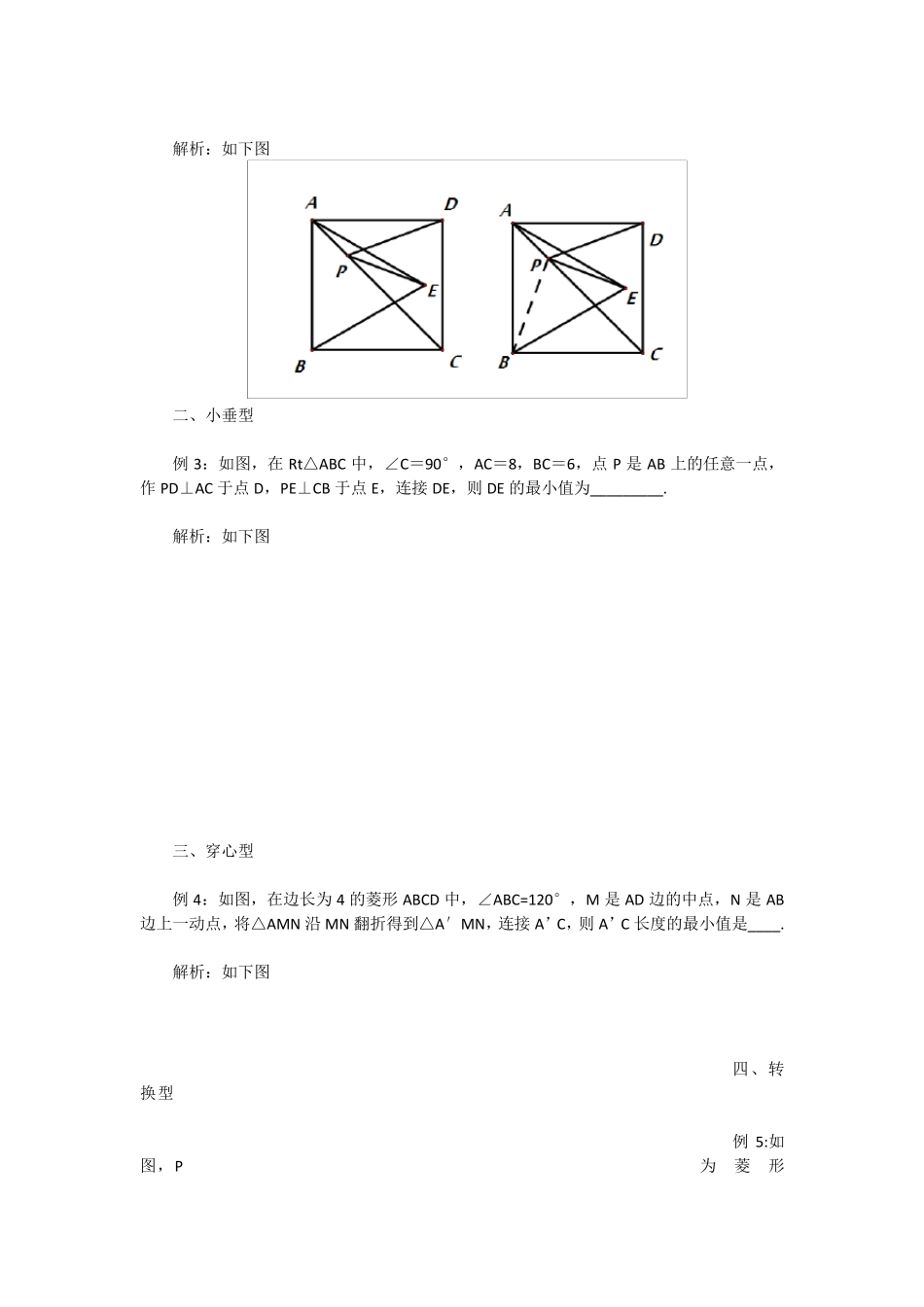
动点最值基本模型 一、最值类型 1.饮马型:即将军饮马型,通常为两条线段之和的最值问题,利用对称性质将其中一条线段进行转换,再利用两点之间线段最短(或三角形三边关系)得到结果。 2.小垂型:即小垂回家型,通常为一条线段的最值问题,即动点的轨迹为直线,利用垂线段最短的性质得到结果。 3.穿心型:即一箭穿心型,通常为一条线段的最值问题,即动点的轨迹为圆或弧,利用点与圆的位置关系得到结果。 4.转换型:即一加半型,通常为一条线段与另一条线段一半的和的最值问题,即将那半条线段利用三角形中位线或30°的对边等知识进行转换,再利用饮马或小垂或穿心。 5.三边型:即三角形三边关系关系型,通常利用两边之和大于第三边、两边之差小于第三边求其最大(小)值。 6.结合型:即以上类型的综合运用,大多为饮马+小垂【如包河一模20 题】【瑶海一模第 10 题】、小垂+穿心【如庐阳二模第 10 题】、饮马+穿心【如瑶海二模第 10 题】饮马+转换【如蜀山二模第 10 题】等 ※二、分类例析 一、饮马型 例 1:如图,在正方形ABCD 中,点E 在 CD 上,CE=3, DE=1, 点P 在 AC 上,则 PE+PD的最小值是_____ . 解析:如图 例 2:如图所示,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD内,在对角线AC 上有一点P,使 PD+PE 的和最小,则这个最小值为____. 解析:如下图 二、小垂型 例3:如图,在Rt△ABC 中,∠C=90°,AC=8,BC=6,点 P 是 AB 上的任意一点,作 PD⊥AC 于点 D,PE⊥CB 于点 E,连接 DE,则 DE 的最小值为_________. 解析:如下图 三、穿心型 例4:如图,在边长为 4 的菱形 ABCD 中,∠ABC=120°,M 是 AD 边的中点,N 是 AB边上一动点,将△AMN 沿 MN 翻折得到△A′MN,连接 A’C,则 A’C 长度的最小值是____. 解析:如下图 四、转换型 例5:如图,P为菱形ABCD 内一点,且P 到A、B 两点的距离相等,若∠C=60°,CD=4,则的最小值为____________ 解析:因为 P 到A、B 两点的距离相等,所以 P 在 AB 的垂直平分线上,又因菱形 ABCD中∠C 为 60°,所以△ABD 为等边三角形,AB 的垂直平分线经过点D,如下图 由∠ADP=30 度,可将 PD 的一半进行转换,即过点P 作 AD 的垂线。如图, 即 B、P、F 三点共线,且BF⊥AD 时最短 五、三边型 例 6:如图,∠MON=90°,矩形 ABCD 的顶点A、B 分别在边 OM,ON 上...