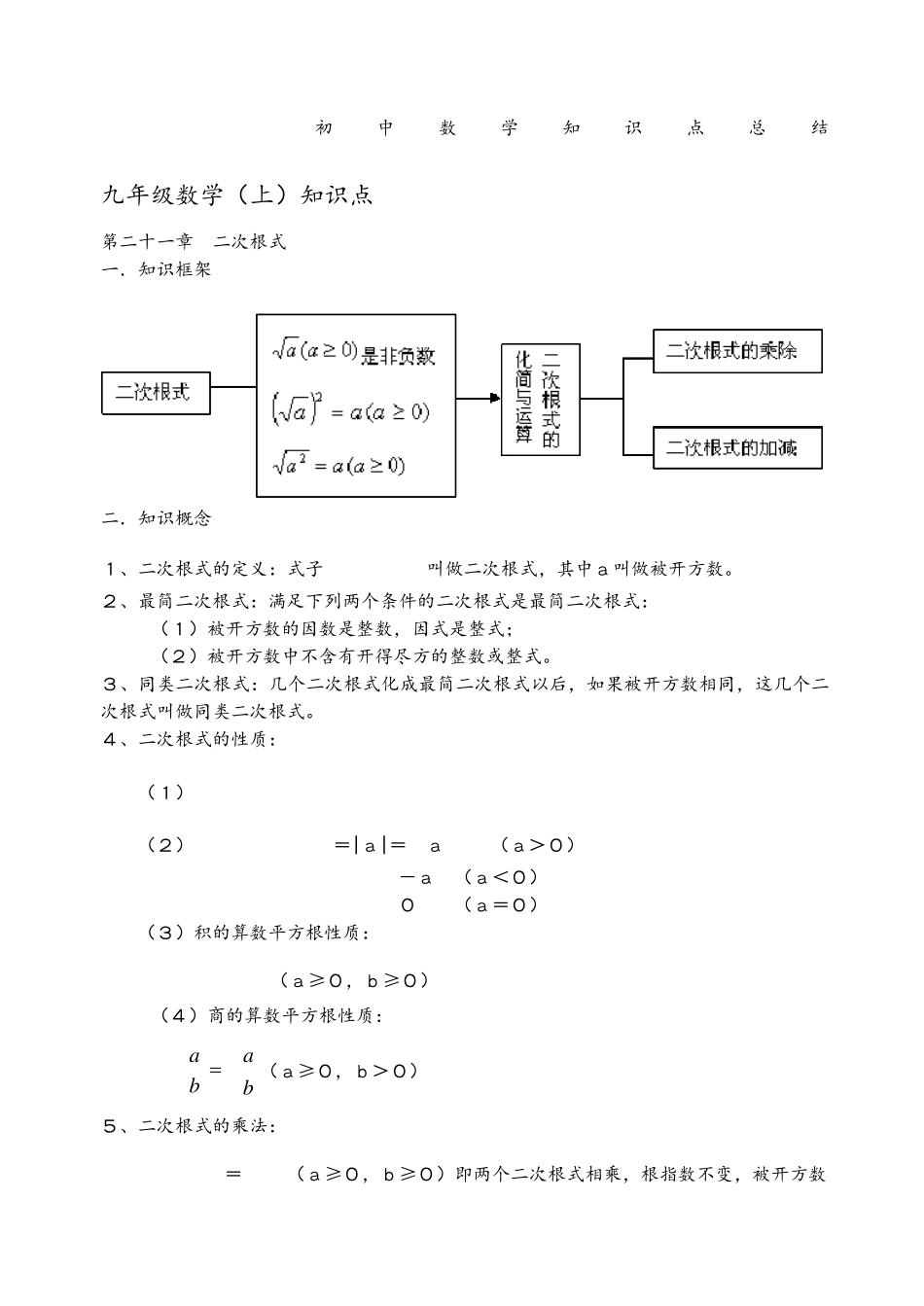
初中数学知识点总结 九年级数学(上)知识点 第二十一章 二次根式 一.知识框架 二.知识概念 1、二次根式的定义:式子叫做二次根式,其中a叫做被开方数。 2、最简二次根式:满足下列两个条件的二次根式是最简二次根式: (1)被开方数的因数是整数,因式是整式; (2)被开方数中不含有开得尽方的整数或整式。 3、同类二次根式:几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式叫做同类二次根式。 4、二次根式的性质: (1) (2)=|a|= a (a>0) -a (a<0) 0 (a=0) (3)积的算数平方根性质: (a≥0,b≥0) (4)商的算数平方根性质: baba (a≥0,b>0) 5、二次根式的乘法: =(a≥0,b≥0)即两个二次根式相乘,根指数不变,被开方数相乘。 注意:法则是由积的算数平方根的性质(a≥0,b≥0)反过来即得。 6、二次根式的除法: baba (a≥0,b>0) 注意:法则是由商的算数平方根的性质baba (a≥0,b>0)反过来得到的。 7、二次根式的加减:二次根式相加减,先把各个二次根式化成最简二次根式,在合并同类二次根式,合并同类二次根式与合并同类项类似,将同类二次根式的“系数”相加减,被开方数和根指数不变。 注意:二次根式加减混合运算的实质就是合并同类二次根式,不是同类二次根式不能合并。 8、二次根式的混合运算: 二次根式的混合运算顺序与实数的运算顺序一样,先乘方,后乘除,最后加减,有括号的先算括号内的。在运算过程中,有理数(式)中的运算率及乘法公式在二次根式的运算中仍然适用。 9、比较两数大小的常用方法: (1)平方法:若a>0,b>0,且a²>b²,则a>b; (2)把跟号外的非负因式移到根号内,然后比较被开方数的大小。 第二十二章 一元二次根式 一.知识框 二.知识概念 1 .一 元 二 次 方 程 : 方 程 两 边 都 是 整 式 , 只 含 有 一 个 未 知 数 ( 一 元 ), 并 且 未 知 数 的 最 高 次数 是 2( 二 次 ) 的 方 程 , 叫 做 一 元 二 次 方 程 . 一 般 地 ,任 何 一 个 关 于 x的 一 元 二 次 方 程 ,• 经 过 整 理 ,• 都 能 化 成 如 下 形 式 ax2+bx+c=0( a≠ 0). 这 种 形 式 叫 做 一 元 二 次 方 程 的 一 般 形 式...