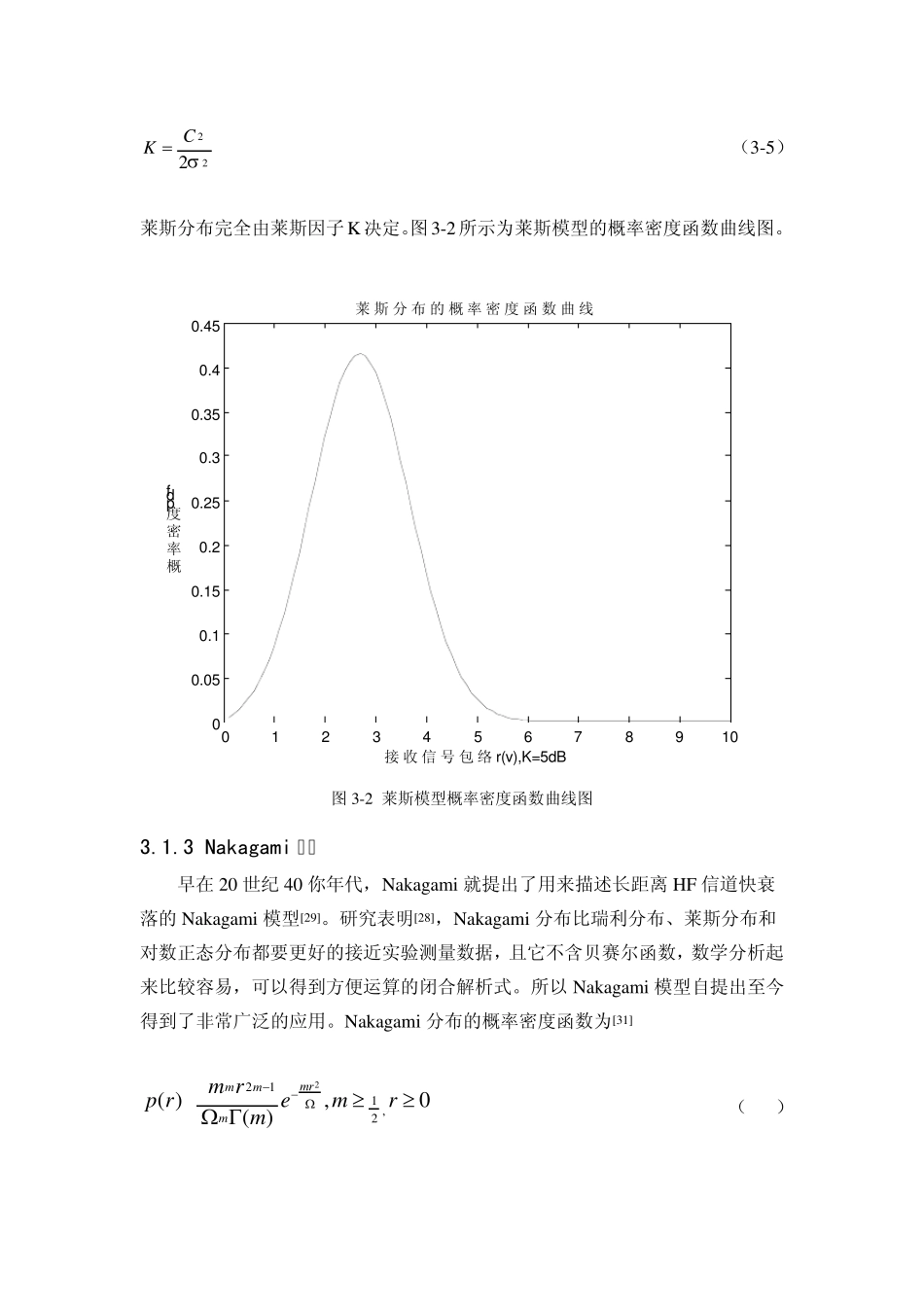
3.1 单状态模型 3.1.1 Rayleigh 模型 在移动无线信道中,瑞利模型是常见的用于描述平坦衰落信号或独立多径分量接收包络统计时变特性的一种经典模型。众所周知,两个正交的正态分布的随机过程之和的包络服从瑞利分布,即设 X 和 Y 为正态随机过程,则 R=X+jY 的包络r =|R|则服从瑞利分布。瑞利分布的概率密度函数(pdf)为[24,27,28]: 0,00,2exp)(222rrrrrp (3-1) 其中,][22rE是包络检波之前的接收信号包络的时间平均功率。R 的相位 θ服从 0 到 2π 之间的均匀分布,即 其他,020,21)(p (3-2) 则接收信号包络不超过某特定值R 的累计概率分布函数(CDF)为 RRdrrpRrpRF0222exp1)()()( (3-3) 图 3-1 所示为瑞利模型的概率密度函数曲线图。 01234567891000.10.20.30.40.50.60.7接收信号包络rpdf瑞利分布包络的概率密度曲线图 图3-1 瑞利模型的概率密度函数曲线图 3.1.2 Ricean 模型 当接收端存在一个主要的静态(非衰落)信号时,如LOS 分量(在郊区和农村等开阔区域中,接收端经常会接收到的)等,此时接收端接收的信号的包络就服从莱斯分布。在这种情况下,从不同角度随机到达的多径分量迭加在静态的主要信号上,即包络检波器的输出端就会在随机的多径分量上迭加一个直流分量。当主要信号分量减弱后,莱斯分布就转变为瑞利分布。莱斯分布的概率密度函数为: 0,00,0,2exp)(202222rrCCrICrrrp (3-4) 其中C 是指主要信号分量的幅度峰值, 0I是 0 阶第一类修正贝赛尔函数。为了更好的分析莱斯分布,定义主信号的功率与多径分量方差之比为莱斯因子 K,则 K 的表达式可以写为 222CK (3-5) 莱斯分布完全由莱斯因子K决定。图3-2所示为莱斯模型的概率密度函数曲线图。 01234567891000.050.10.150.20.250.30.350.40.45接收信号包络r(v ),K=5dB概率密度pdf莱斯分布的概率密度函数曲线 图3-2 莱斯模型概率密度函数曲线图 3.1.3 Nakagami 模型 早在20 世纪40 你年代,Nakagam i 就提出了用来描述长距离HF 信道快衰落的Nakagam i 模型[29]。研究表明[28],Nakagam i 分布比瑞利分布、莱斯分布和对数正态分布都要更好的接近实验测量数据,且它不含贝赛尔函数,数学分析起来比较容易,可以得到方便运算的闭合解...