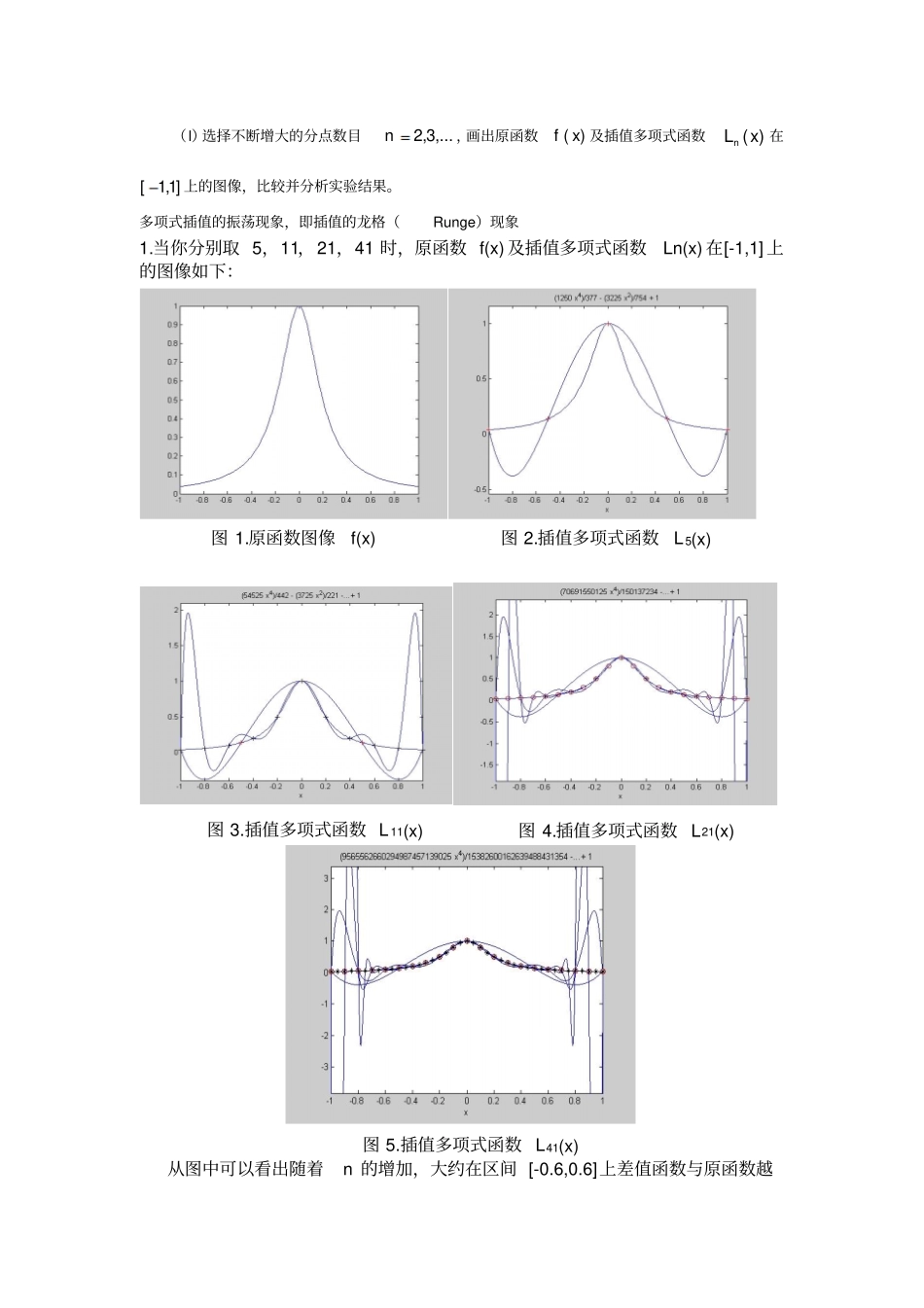
数值计算方法上机题目1 1、实验 1. 病态问题1、实验 1. 病态问题实验目的 :算法有“优”与“劣”之分,问题也有“好”和“坏”之别。所谓坏问题就是问题本身的解对数据变化的比较敏感,反之属于好问题。 希望读者通过本实验对此有一个初步的体会。数值分析的大部分研究课题中,如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。病态问题要通过研究和构造特殊的算法来解决,当然一般要付出一些代价(如耗用更多的机器时间、占用更多的存储空间等)。问题提出 :考虑一个高次的代数多项式201)()20)...(2)(1()(kkxxxxxp(E1-1)显然该多项式的全部根为l,2,⋯, 20,共计 20 个,且每个根都是单重的(也称为简单的)。现考虑该多项式方程的一个扰动0)(19xxp(E1-2) 其中是一个非常小的数。这相当于是对(E1-1)中19x的系数作一个小的扰动。我们希望比较( E1-1)和( E1-2)根的差别,从而分析方程(E1-1)的解对扰动的敏感性。实验内容 :为了实现方便,我们先介绍两个Matlab 函数:“roots”和“ poly”,输入函数u=roots(a)其中若变量 a 存储1n维的向量,则该函数的输出u 为一个 n 维的向量。设a 的元素依次为121,...,,naaa,则输出 u 的各分量是多项式方程0...1121nnnnaxaxaxa的全部根,而函数b=poly(v) 的输出 b 是一个 n+1 维变量,它是以 n 维变量 v 的各分量为根的多项式的系数。可见“roots”和“ Poly”是两个互逆的运算函数. ve=zeros(1,21); ve(2)=ess; roots(poly(1:20))+ve) 上述简单的Matlab 程序便得到 (E1-2)的全部根, 程序中的 “ess”即是(E1-2)中的。实验要求 :(1)选择充分小的ess,反复进行上述实验,记录结果的变化并分析它们。如果扰动项的系数很小,我们自然感觉(E1-1)和 (E1-2)的解应当相差很小。计算中你有什么出乎意料的发现?表明有些解关于如此的扰动敏感性如何?1.如程序 Wjj-1.m 所示,给19x的系数一个扰动时,解会产生变化。扰动越小,解与真实值越接近。当扰动增加到一定值,解会变成负数,在所做的给19x的系数一个扰动的实验中,当该扰动大于10^-11 时,产生复数解。2.将扰动项改成18x,解同样会发生变化。扰动越小,解的变化越小,当扰动增加到一定值,解会变成负数,在所做的给18x的系数一个扰动的实验中,当该扰动大于 10^-9 时,产生复数解。3.解关于的导数的绝对值越大,解关于的扰动越敏感。 18、17、16、15、1...