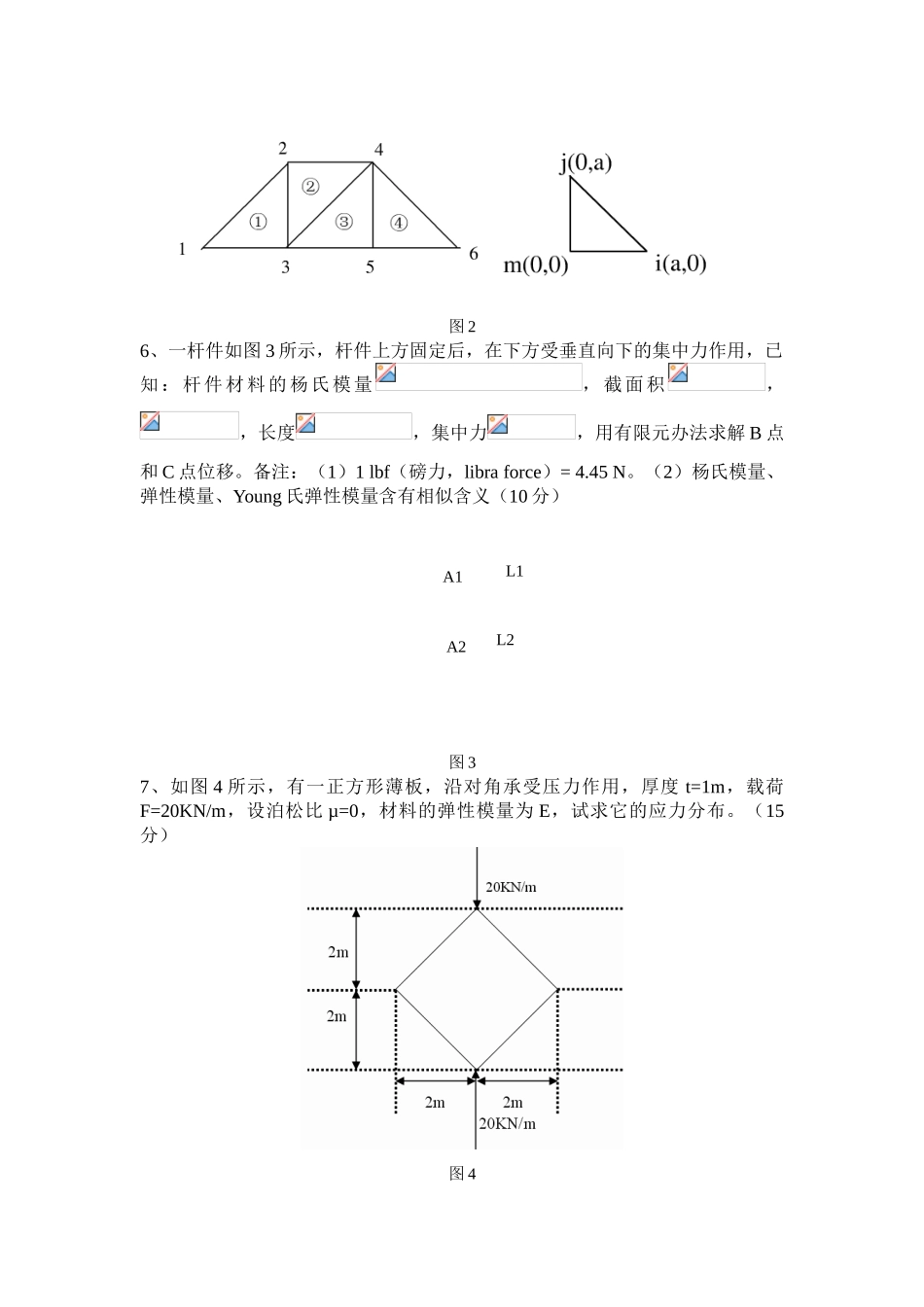
江西理工大学硕士考试试卷1、将任意单元映射为单位长度的单元,通过这种映射关系推导一维拉压杆件单元的单元刚度矩阵。(10 分)2、平面等参数单元中的“等参数”概念的意义?该单元在跨相邻单元时,位移场和应力场持续性如何?(10 分)3、用有限元办法平面正方形自重应力场,边界约束条件为下边界垂直方向约束,侧边水平方向约束,上边界为自由边界。(15 分)4、如图 1 所示,等腰直角三角形单元,其厚度为 t,弹性模量为 E,泊松比;单元的边长及节点编号如图,求(1)形函数矩阵;(2)应变矩阵和应力矩阵;(3)单元刚度矩阵。(10 分)图 15、求图 2 中的总刚度矩阵(5 分)20__12__—20__13__ 年 第___一___学期课程名称:_____有限元及数值模拟________考试时间:______ 年__11__月___3___日考试性质(正考、补考或其它):[ 正考 ]考试方式(开卷、闭卷):[ 开卷 ]试卷类别(A、B):[ A ] 共 九 大题温 馨 提 示请考生自觉恪守考试纪律,争做文明诚信的大学生。如有违犯考试纪律,将严格按照《江西理工大学学生违纪处分规定》(试行)解决。学院 专业 学号 姓名 题号一二三四五六七八九十十一十二总 分得分图 26、一杆件如图 3 所示,杆件上方固定后,在下方受垂直向下的集中力作用,已知:杆件材料的杨氏模量,截面积,,长度,集中力,用有限元办法求解 B 点和 C 点位移。备注:(1)1 lbf(磅力,libra force)= 4.45 N。(2)杨氏模量、弹性模量、Young 氏弹性模量含有相似含义(10 分)图 37、如图 4 所示,有一正方形薄板,沿对角承受压力作用,厚度 t=1m,载荷F=20KN/m,设泊松比 µ=0,材料的弹性模量为 E,试求它的应力分布。(15分)图 4A1A2L1L28、如图 5 下梯形悬臂梁,计算需要的几何及物理力学参数自己定,不计体积力。(10 分)图 59、用二维等参单元对处在平面应力的短悬臂梁进行静力分析,梁的长度和高度分别为 8m 和 1m,E=1.0e+6 Pa。µ=0.3,梁端部集中荷载为 1KN。(15 分)图 61 2 3 4 5 6 7 8 9 10 11⑦①③②⑤④⑩⑥⑨⑧P