空间几何体的外接球VIP免费

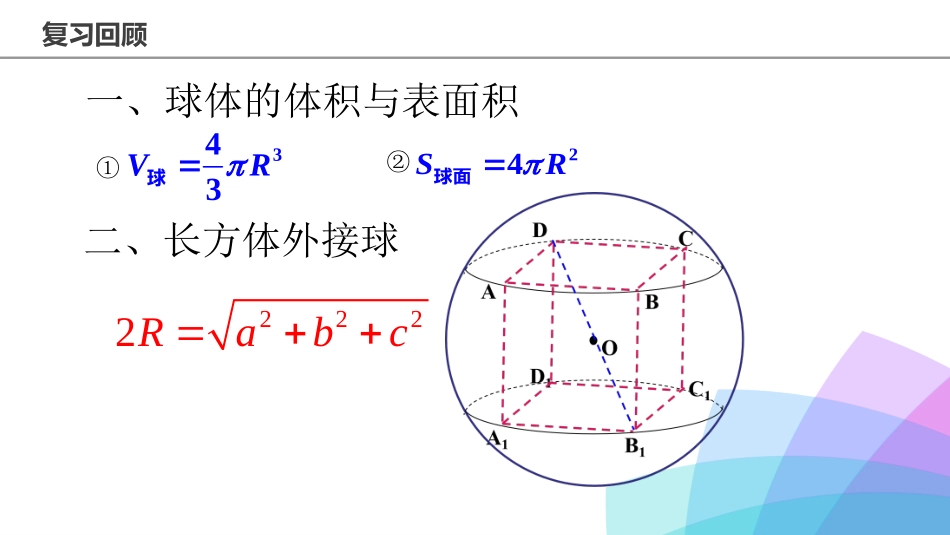
微专题：空间几何体的外接球20152017201820192020感悟高考近几年新课标全国卷空间几何体外接球试题在题型、考查载体、考查能力、解题方法等方面呈现怎样的特征?01考查以选择、填空题形式；难度中等；02载体以柱体、锥体为主，对空间想象能力要求较高；03解题关键是找出球心、半径与其它线面关系;04熟悉常见模型，将空间问题平面化.复习回顾一、球体的体积与表面积343VR球①24SR球面②2222Rabc二、长方体外接球复习回顾三、球体相关性质OO1O2典型例题2383334V例1（1）正四面体的各条棱长都为2，则该正面体外接球的体积为.典型例题（2）在三棱锥BCDA中，,4,3,2BDACBCADCDAB则三棱锥BCDA外接球的表面积为.229思考？yxabczzyxDCAByxabczzyxDCAB第一步：画出一个长方体，标出三组互为异面直线的对棱；第二步：设出长方体的长宽高分别为cba,,，xBCAD，yCDAB，zBDAC，列方程组，222222222zacycbxba2)2(2222222zyxcbaR，第三步：根据22222222zyxcbaR，求出R。对棱相等，补全为长方体例2（1）若三棱锥的三条侧棱两两垂直，且侧棱长均为，则其外接球的表面积是.典型例题9π典型例题解：引理：正三棱锥的对棱互垂直。证明如下：如图（3）-1，取BCAB,的中点ED,，连接CDAE,，CDAE,交于H，连接SH，则H是底面正三角形ABC的中心，SH平面ABC，ABSH，BCAC，BDAD，ABCD，AB平面SCD，SCAB，同理：SABC，SBAC，即正三棱锥的对棱互垂直，本题图如图（3）-2，MNAM，MNSB//，SBAM，SBAC，SB平面SAC，SASB，SCSB，SASB，SABC，SA平面SBC，SCSA，故三棱锥ABCS的三棱条侧棱两两互相垂直，36)32()32()32()2(2222R，即3642R，正三棱锥ABCS外接球的表面积是36思考？MNABCS（2）在正三棱锥SABC中，MN、分别是棱SCBC、的中点，且MNAM,若侧棱23SA,则正三棱锥ABCS外接球的表面积是。36πcabCPAB方法：找三条两两垂直的线段，直接用公式2222)2(cbaR，即2222cbaR，求出RabcPCBAabcPCO2BA例3（1）已知各顶点都在同一球面上的正四棱柱的高为4，体积为16，则这个球的表面积是（）A．16B．20C．24D．32CAA1B1C1D1DCBO2O1O(2)在四面体SABC中，ABCSA平面，,1,2,120ABACSABAC则该四面体的外接球的表面积为（）11.A7.B310.C340.DABCSDO2O1OC1B1AA1O1OO2BCC1B1AA1O1OO2BCC1B1AA1O1OO2BC如图1，2，3,直三棱柱内接于球（同时直棱柱也内接于圆柱，棱柱的上下底面可以是任意三角形）第一步：确定球心O的位置，1O是ABC的外心，则1OO平面ABC；第二步：算出小圆1O的半径rAO1，hAAOO212111（hAA1也是圆柱的高）；第三步：勾股定理：21212OOAOOA222)2(rhR22)2(hrR，解出R典型例题例4正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为32，则该球的表面积为。典型例题例4正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为32，则该球的表面积为。121𝜋4图6PADO1OCB解题步骤：第一步：确定球心O的位置，取ABC的外心1O，则1,,OOP三点共线；第二步：先算出小圆1O的半径rAO1，再算出棱锥的高hPO1（也是圆锥的高）；第三步：勾股定理：21212OOAOOA222)(rRhR，解出R例5已知PAB所在的平面与矩形ABCD所在的平面互相垂直，60,2,3APBADPBPA，则多面体ABCDP的外接球的表面积为。BACDEF16πPDCABO2O1O典型例题变式1将上题中条件“矩形ABCD”改为“正三角形ABC”，则多面体ABCP的外接球的表面积为。解析：3460sin22221rr，3221rr，312HO，35343121222rHOR，315R；法二：312HO，311HO，1AH，352121222OOHOAHAOR，315ROHBACPO2O1APBC15π典型例题变式23DABC21πOO2MO1O1OMO2H1EACOBDA'H2第一步：先画出如图所示的图形，将BCD画在小圆上，找出BCD和BDA的外心1H和2H；第二步：过1H和2H分别作平面BCD和平面BDA的垂线，两垂线的交点即为球心O，连接OCOE,；第三步：解1OEH，算出1OH，在1OCHRt中，勾股定理：22121OCCHOH思考？链接高考1.链接高考链接高考2．(2020·全国Ⅰ)已知A，B，C为球O的球面上的三个点，⊙O1为△ABC的外接圆．若⊙O1的面积为4π，AB＝BC＝AC＝OO1，则球O的表面积为()A．64πB．48πC．36πD．32π