线性代数期末考试试卷(标准参考题)VIP免费

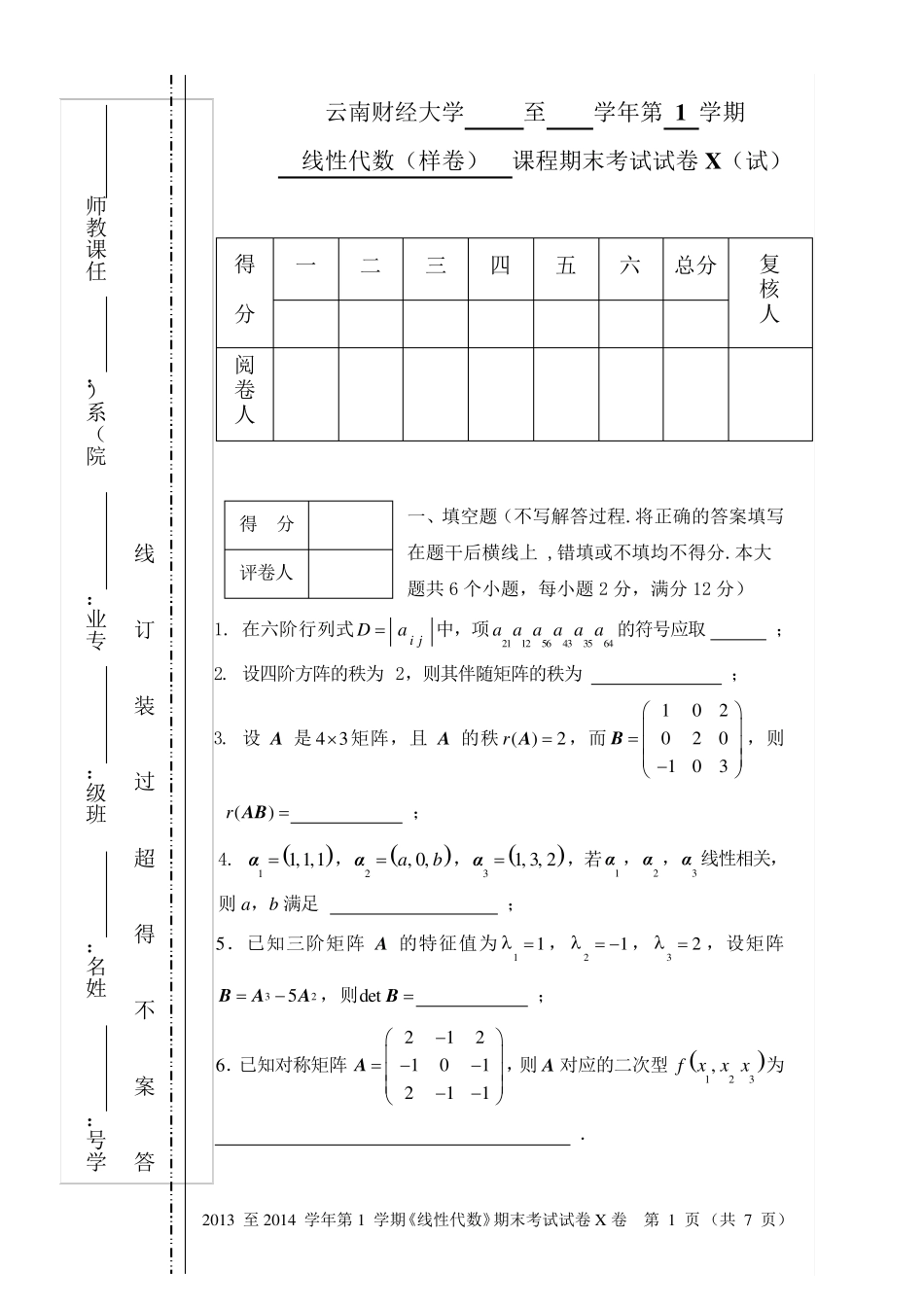
2013 至2014 学年第1 学期《线性代数》期末考试试卷X 卷 第 1 页 （共 7 页） 一、填空题（不写解答过程.将正确的答案填写 在题干后横线上 ,错填或不填均不得分.本大 题共6 个小题，每小题 2 分，满分 12 分） 1. 在六阶行列式i jDa中，项211256433564a a a a a a 的符号应取 ； 2. 设四阶方阵的秩为 2，则其伴随矩阵的秩为 ； 3. 设 A 是 4 3 矩阵，且 A 的秩 ( )2rA，而102020103 B，则()rAB ； 4. 11,1,1α，2, 0,abα，31, 3, 2α，若1α ，2α ，3α 线性相关，则 a，b 满足 ； 5．已知三阶矩阵 A 的特征值为11 ，21  ，32，设矩阵325BAA ，则detB ； 6．已知对称矩阵212101211A，则 A 对应的二次型123,f xx x为 ． 得 分 评卷人 云南财经大学 至 学年第 1 学期 线性代数（样卷） 课程期末考试试卷X （试） 得 分 一 二 三 四 五 六 总分 复 核 人 阅 卷 人 学号： 姓名： 班级： 专业： 院（系）： 任课教师 答 案 不 得 超 过 装 订 线 2013 至2014 学年第1 学期《线性代数》期末考试试卷X 卷 第 2 页 （共 7 页） 二、单选题（不写解答过程.在每小题列出的四个选项中只 有一个符合题目要求，请将其代码填在括号内,错选或末选 均不得分.本大题共6 个小题，每小题2 分，满分12 分） 1. 已知1112132122233132333aaaaaaaaa，113121211333232312322222253253253aaaaaaaaaaaa（ ）； （A）18； （B）18； （C）9； （D）90． 2．设11121314212223243132333441424344aaaaaaaaaaaaaaaa A，14131211242322213433323144434241aaaaaaaaaaaaaaaa B，10001010000101000 P，21000001001000001 P，其中A 可逆，则1 B（ ）； （A）112A P P ； （B）112P A P ； （C）121P A P ； （D）112P P A ． 3．设A，B 为n 阶方阵，且满足AB =0，则必有（ ）； （A）0A或0B； （B）det0A或det0B； （C）222ABAB ； （D）A，B 均不可逆． 4．已知1α ，2α ，3α 是齐次线性方程组AX0 的基础解系，那么它...