线性代数第一章习题集VIP免费

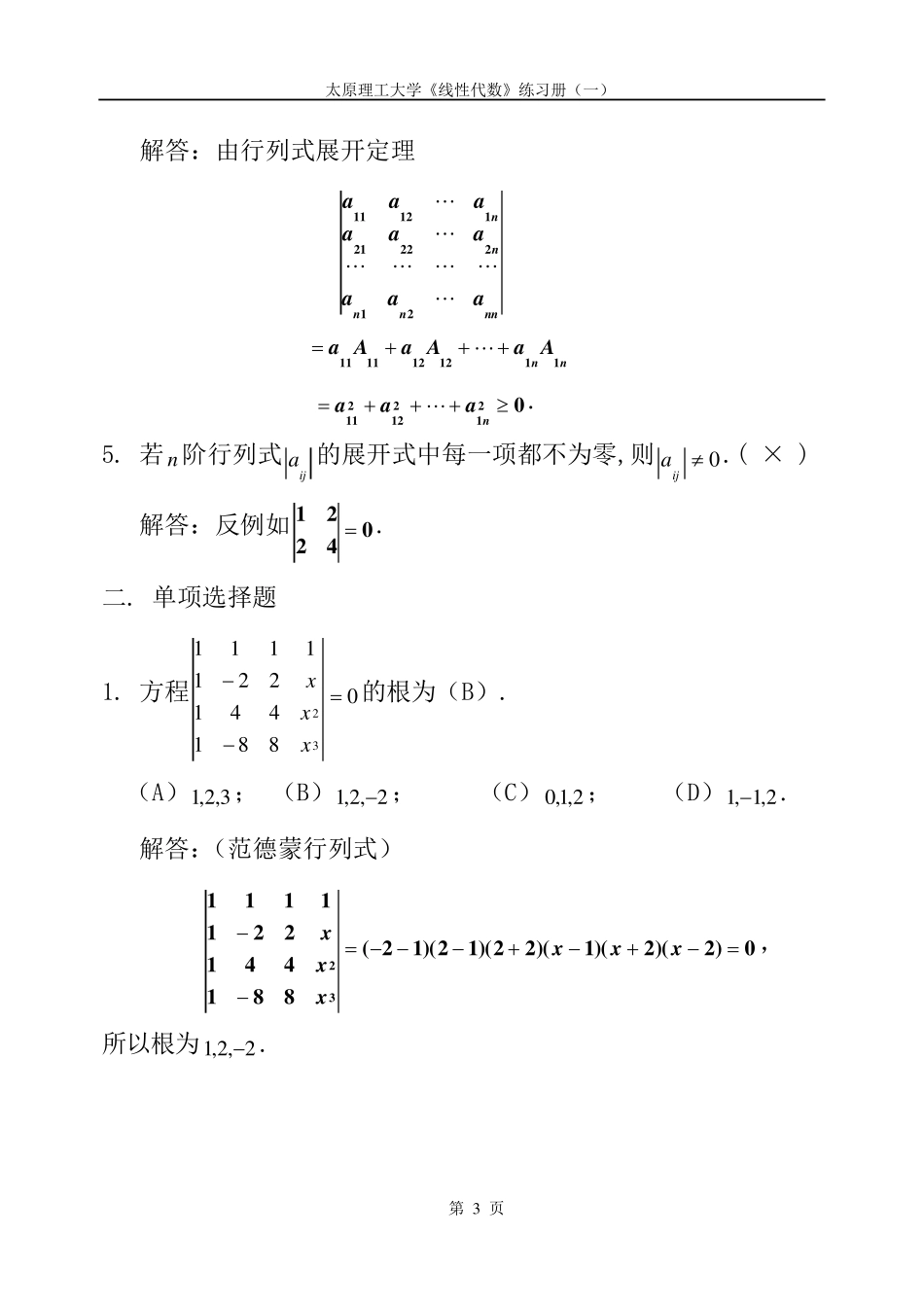
太原理工大学《线性代数》练习册（一） 第 1 页 一. 判断题（正确打√，错误打×） 1. n 阶行列式ija 的展开式中含有1 1a 的项数为1n.( × ) 正确答案：)!1( n 解答：方法 1 因为含有1 1a 的项的一般形式是nn jjaaa221 1， 其中njjj32是1n级全排列的全体，所以共有)!1( n项. 方法 2 由行列式展开定理 n nnnnnaaaaaaaaa2122 22 111 21 1nn AaAaAa1121211111， 而nn AaAa112121 中不再含有1 1a ，而1 1A 共有)!1( n项，所以含有1 1a 的项数是)!1( n. 注意：含有任何元素ija 的项数都是)!1( n. 2. 若n 阶行列式ija 中每行元素之和均为零，则ija 等于零.( √ ) 解答：将n nnnnnaaaaaaaaa2122 22 111 21 1中的n、、、 32列都加到第一列，则行 列式中有一列元素全为零，所以ija 等于零. 太原理工大学《线性代数》练习册（一） 第 2 页 3.332244114433221100000000abbaabbaababbaba.( √ ) 解答：方法 1 按第一列展开 332244114411414133224133224144332211)(00000000abbaabbaabbabbaaabbabbabbaaaababbaba. 方法 2 交换 2，4 列，再交换 2，4 行 223344114433221144332211000000000000000000000000abbaabbaabbaabbaababbaba=33224411abbaabba. 方 法 3 Laplace 展 开 定 理： 设 在 n 行 列 式 D 中 任 意 取 定 了)11(nkk个行，由这 k 行元素所组成的一切 k 阶子式与它们的代数余子式的乘积之和等于行列式 D。 所以按 2，3 行展开 323244332211)1(00000000ababbaba33224411abbaabba=33224411abbaabba. 4. 若n 阶行列式ija 满足ijijAa ,nji，，,2,1,则0ija.(√) 太原理工大学《线性代数》练习册（一） 第 3 页 解答：由行列式展开定理 nnnnnnaaaaaaaaa2122 22 111 21 1 nnAaAaAa1121211111 02121 221 1naaa. 5. 若n 阶行列式ija 的展开式中每一项都不为零,则0ija.( × ) 解答：反例如04221 . 二. 单项选择题 1. 方程0881441221111132 xxx的根为（B）. （A）3,2,1； （B）2,2,1 ； （C）2,1,0； （D）2,1,1 . 解答：（范德蒙行列式） 0)2)(2)(1)(22)(12)(12(881441221111132xxxxxx， 所以根为2,2,1...