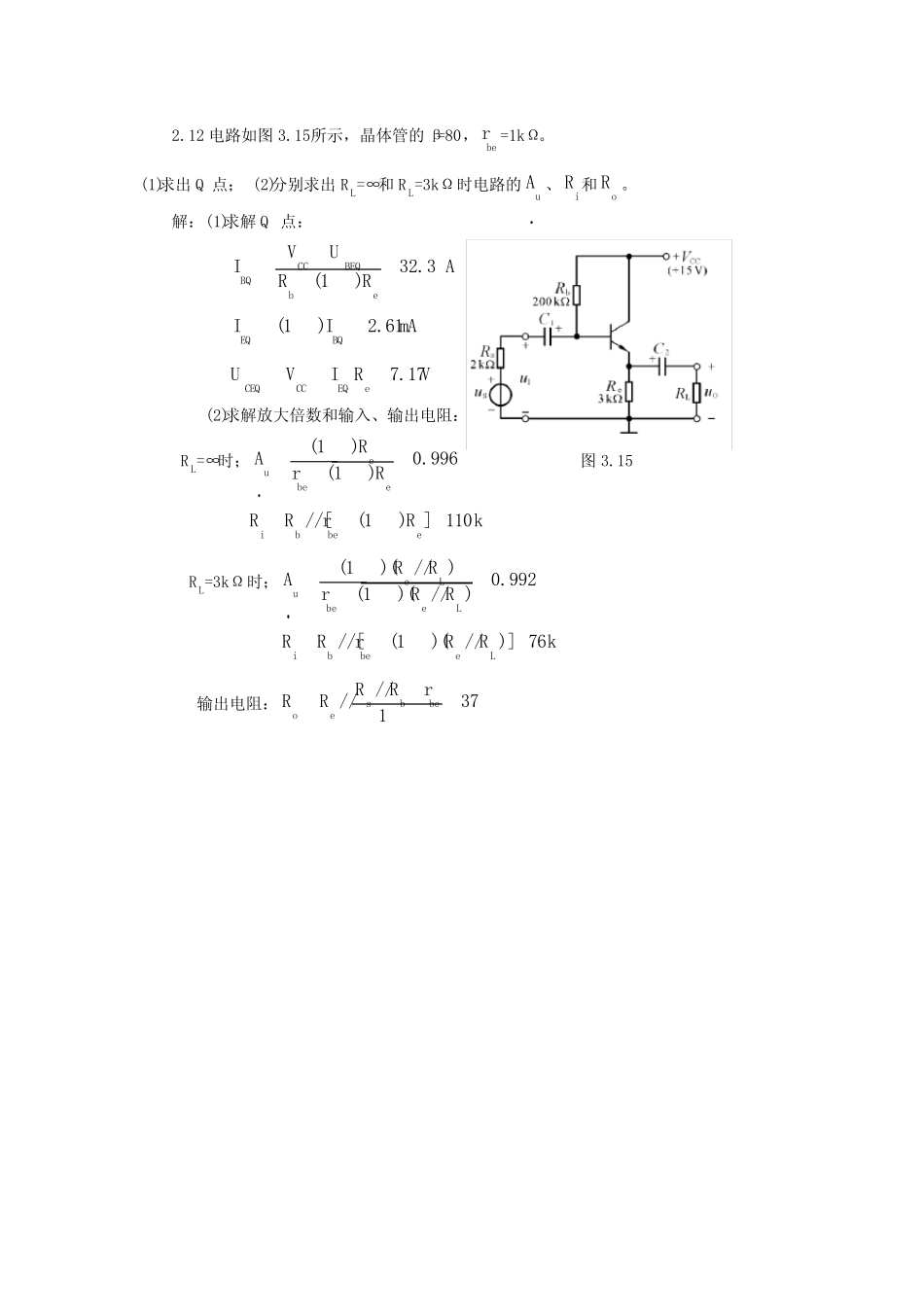
2.12 电 路 如 图 3.15所 示 , 晶 体 管 的 β=80,ber =1kΩ 。 (1)求 出 Q 点 ; (2)分 别 求 出 R L=∞ 和 R L=3kΩ 时 电 路 的uA 、iR 和oR 。 解 : (1)求 解 Q 点 : 32.3(1)CCBEQBQbeVUIARR (1)2.61EQBQIImA 7.17CEQCCEQeUVI RV (2)求 解 放 大 倍 数 和 输 入 、 输 出 电 阻 : R L=∞ 时 ;(1)0.996(1)eubeeRArR 图 3.15 //[(1)] 110ibbeeRRrRk R L=3kΩ 时 ;(1)(//)0.992(1)(//)eLubeeLRRArRR //[(1)(//)] 76ibbeeLRRrRRk 输 出 电 阻 :////371sbbeoeRRrRR 2.11 电 路 如 图 P2.11所 示 , 晶 体 管 β=100,bbr=100Ω 。 (1)求 电 路 的 Q 点 、uA、iR 和oR ; (2)若 电 容 C e开 路 , 则 将 引 起 电 路 的 哪 些 动 态 参 数 发 生 变 化 ? 如 何 变 化 ? 解 : (1)静 态 分 析 : 1122bBQCCbbRUVVRR 1BQBEQEQfeUUImARR 101EQBQIIA e(R ) 5.7CEQCCEQcfUVIRRV 图 P2.11 动 态 分 析 :'26(1)2.73bebbEQmVrrkI (//)7.7(1)cLubefRRArR 12////[(1)] 3.7ibbbefRRRrRk 5ocRRk (2) Ce开 路 时 ,(//)//1.92(1)()cLcLubeefefRRRRArRRRR ( 减 小 ); 12////[(1)()] 4.1ibbbeefRRRrRRk ( 增 大 ); 5ocRRk ( 不 变 )。 3.23 在 图 所 示 电 路 中 , 已 知V CC =16V , R L=4Ω , T1 和T2 管 的 饱 和 压 降CESU=2V , 输 入 电压 足 够 大 。 试 问 : (1)最 大 输 出 功 率 P om 和 效 率 η 各 为 多 少 ? (2)晶 体 管 的 最 大 功 耗 P Tmax 为 多 少 ? (3)为 了 使 输 出 功 率 达 到 P om , 输 入 电 压 的 有 效 值 约 为 多 少 ? 解 : (1)最 大 输 出 功 率 和 效 率 分 别 为 2()24.52CCCESomLVUPWR, 69.8%4CCCESCCVUV (2)晶 体 管 的 最 大 功 耗 2max0.20.26.42CCTomLVPPWR (3)输 出 功 率 为 P om 时 的 输 入 电 压 有 效 值 9.92CCCESiomVUUUV 5.6 求 图 5.6所 示 的 电 路 中 u0 与 各 输 入 电 压 的 运 算 关 系 式 。 解 : 对 半 左 边 部 分 电 路 为 反 相 比 例 运 算 电 路 , 所 以 依 题 意 可 得 : u01=- RF/ R1* u11=-10 u11 对 右 半 部 分 电 路 为 反 相 加 法 运 算 电 路 , 所 以 有 : u0=-( RF/ R11* u11+ RF/ R12* u12+ RF/ R13* u13) =-( 10/ 10* u01+ 10/ 5* u12+ 10/ 2* u13) =-( -10u11+ 2u12+ 5u13) =10u11-2u12-5u13