压杆稳定性计算汇总精编版VIP免费

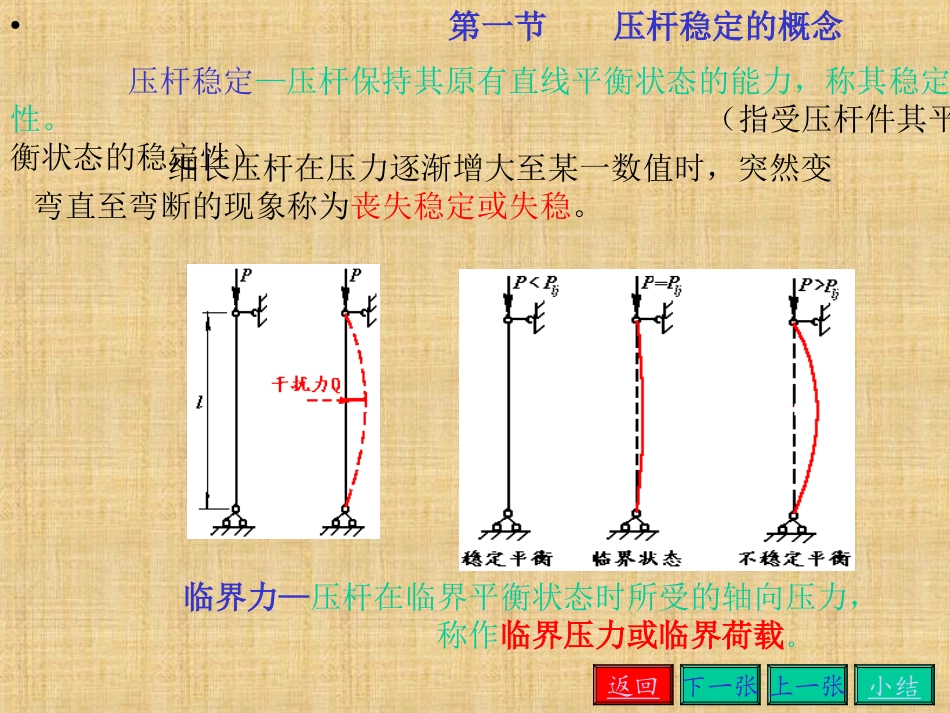
•第第1111章压杆稳定章压杆稳定返回压杆稳定的概念细长压杆的临界力压杆的临界应力压杆的稳定计算提高压杆稳定的措施小结第一节第二节第三节第四节第五节•第一节压杆稳定的概念压杆稳定—压杆保持其原有直线平衡状态的能力，称其稳定性。（指受压杆件其平衡状态的稳定性）临界力—压杆在临界平衡状态时所受的轴向压力，称作临界压力或临界荷载。细长压杆在压力逐渐增大至某一数值时，突然变弯直至弯断的现象称为丧失稳定或失稳。返回下一张上一张小结一、两端铰支细长压杆的临界力第二节细长压杆的临界力取X截面研究弹性范围内的挠曲线方程：;)(22yEIPEIxMdxydlj;0,2222ykdxydkEIPlj则有令;cossin21kxckxcy其通解为;0sin;0;0,;0,012klccylxyx得由边界条件);210()210(;0sin,02221nnlEInPnnnklklclj、、、则；、、、得所以因为22lEIPlj所以取取不为零的最小值，即,1nn—两端铰支细长压杆的临界力计算公式（欧拉公式）返回下一张上一张小结2min2)(lEIPlj式中：E材料的弹性模量；Imin压杆横截面对中性轴的最小惯性矩；单位：m4；μl计算长度；长度系数，与杆端支承有关。一端固定，一端自由压杆：μ＝2；两端铰支细长压杆：μ＝1；一端固定，一端铰支压杆：μ＝0.7；两端固定细长压杆：μ＝0.5；二、其他支承情况下细长压杆的临界力不同支承情况的压杆其边界条件不同，临界力值也不同。也可由挠曲线比较得出欧拉公式的通式：不同支承情况的临界力公式可查表确定。返回下一张上一张小结下一张上一张返回小结•例10-1一根两端铰支的20a号工字钢压杆，长L=3m，钢的弹性模量E=200GPa，试确定其临界压力。22lEIpljkNlEIPlj34631015810200286222下一张上一张返回小结•解：查表得20a号工字钢:Iz=2370cm4,Iy=158cm4,•临界压力按公式计算•由此可知，若轴向压力达到346KN时，此压杆便会丧失稳定。•例10-2：截面为200×120mm2的轴向受压木柱，l=8m，柱的支承情况是，在最大刚度平面内压弯时为两端铰支（图a）；在最小刚度平面内压弯时为两端固定（图b），木材的弹性模量E=10GPa，试求木柱的临界压力。解：由于柱在最大与最小刚度平面内压弯时的支承情况不同，所以需要分别计算在两个平面内失稳的临界压力，以便确定在哪个平面内失稳。（1）计算最大刚度平面内的临界压力（即绕y轴失稳）。中性轴为y轴：Iy=120×2003/12=80×106mm4=80×10-6m4木柱两端铰支，，则得：kNlEIPylj123800011080101014.3263222下一张上一张返回小结•（2）计算最小刚度平面内的临界压力（即绕z轴失稳）。•中性轴为z轴：46463108.28108.2812120200mmmIz木柱两端固定，，则得：比较计算结果可知：第一种情况临界压力小，所以木柱将在最大刚度平面内失稳（即绕y轴，在xoz平面内失稳）。此例说明，当最小刚度平面和最大刚度平面内支承情况不同时，压杆不一定在最小刚度平面内失稳，必须经过计算才能最后确定。KNlEIPzlj17880005.0108.28101014.3263222下一张上一张返回小结第三节压杆的临界应力一、临界应力与柔度222222222EilEAIlEAlEIAPljlj临界应力—临界压力作用下压杆处于临界直线平衡状态时的应力。面的几何性质；截面的惯性半径；为截—其中：AIi程度。比）；反映压杆的柔软称为压杆的柔度（长细＝il二、欧拉公式的适用范围pppljEE222或λp—分界柔度，取决与材料的力学性质。A3钢：100200200000,200,2002ppEPaGPaE下一张上一张返回小结三、超出比例极限时压杆的临界力临界应力总图;)(;22AbaAPbaljljlj当临界应力超出比例极限时，材料处于弹塑性阶段，此类压杆的稳定称弹塑性稳定。临界应力由经验公式计算。式中：λ—压杆的长细比；a、b—与材料有关的常数,可查表确定。A3钢：a＝235,b＝0.00668；16锰钢：a＝343,b＝0.0142。临界应力总图—临界应力lj与柔度的函数关系曲线。;:;:222...