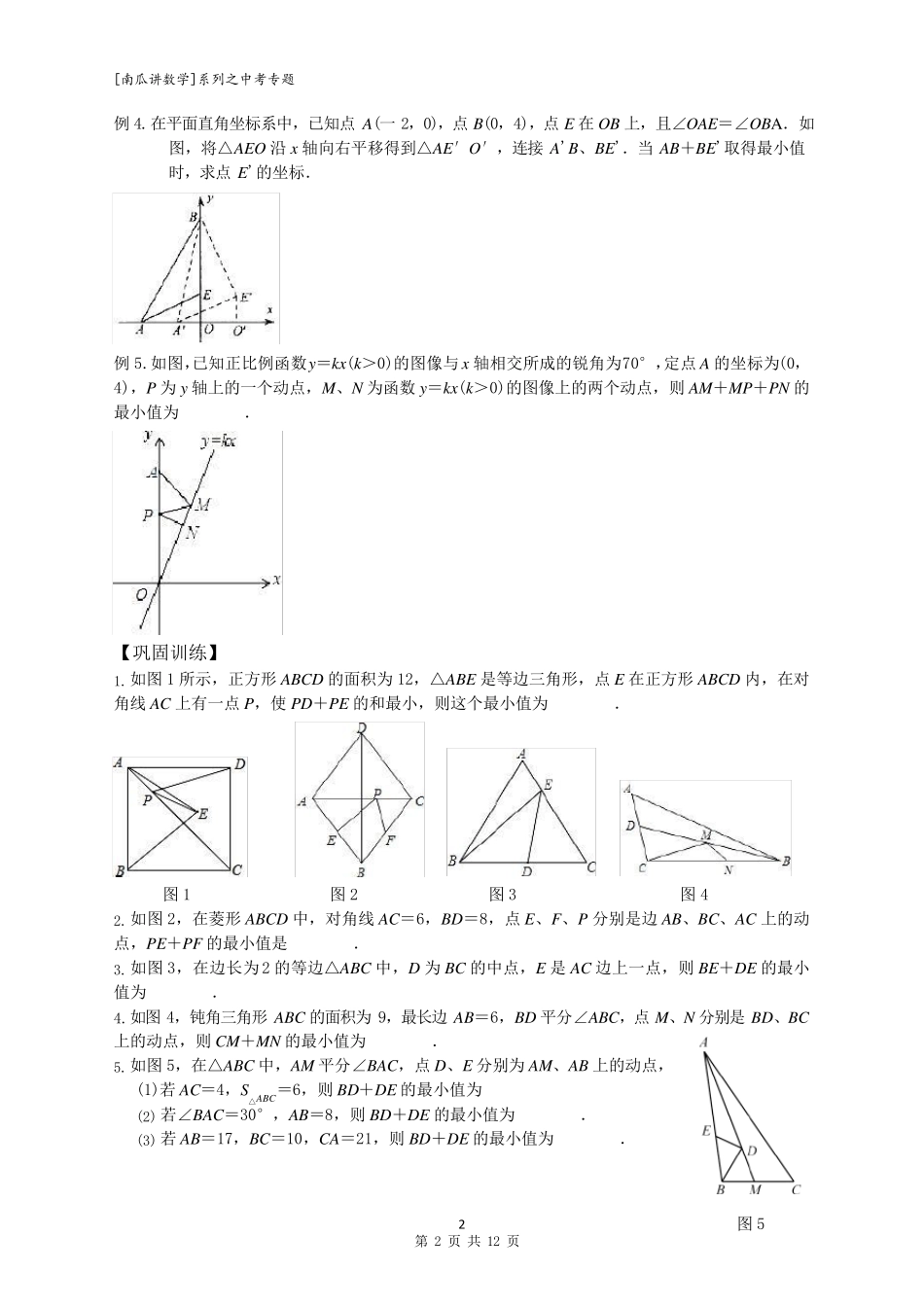
1 第 1 页 共 12 页 【模型解析】 2020 中考专题 8——最值问题之将军饮马 班级 姓名 . 总结:以上四图为常见的轴对称类最短路程问题,最后都转化到:“两点之间,线段最短”解决。 特点:①动点在直线上;②起点,终点固定; 方法:作定点关于动点所在直线的对称点。 【例题分析】 例 1.如图,在平面直角坐标系中,Rt△OAB 的顶点 A 在 x 轴的正半轴上,顶点 B 的坐标为(3, 3 ), 点 C 的坐标为( 1 ,0),点 2 P 为斜边 OB 上的一动点,则 PA+PC 的最小值为 . 例 2.如图,在五边形 ABCDE 中,∠BAE=120°,∠B=∠E=90°,AB=BC=1,AE=DE=2, 在 BC、DE 上分别找一点 M、N. (1)当△AMN 的周长最小时,∠AMN+∠ANM= ; (2)求△AMN 的周长最小值. 例 3.如图,正方形 ABCD 的边长为 4,点 E 在边 BC 上且 CE=1,长为 2 的线段 MN 在 AC 上运动. (1) 求四边形 BMNE 周长最小值; (2) 当四边形 BMNE 的周长最小时,则 tan∠MBC 的值为 . [南瓜讲数学]系列之中考专题 2 图 5 第 2 页 共 12 页 例 4.在平面直角坐标系中,已知点 A(一 2,0),点 B(0,4),点 E 在 OB 上,且∠OAE=∠OBA .如图,将△AEO 沿 x 轴向右平移得到△AE′O′,连接 A'B、BE'.当 AB+BE'取得最小值时,求点 E'的坐标. 例 5.如图,已知正比例函数 y=kx(k>0)的图像与 x 轴相交所成的锐角为 70°,定点 A 的坐标为(0, 4),P 为 y 轴上的一个动点,M、N 为函数 y=kx(k>0)的图像上的两个动点,则 AM+MP+PN 的最小值为 . 【巩固训练】 1. 如图 1 所示,正方形 ABCD 的面积为 12,△ABE 是等边三角形,点 E 在正方形 ABCD 内,在对角线 AC 上有一点 P,使 PD+PE 的和最小,则这个最小值为 . 图 1 图 2 图 3 图 4 2. 如图 2,在菱形 ABCD 中,对角线 AC=6,BD=8,点 E、F、P 分别是边 AB、BC、AC 上的动点,PE+PF 的最小值是 . 3. 如图 3,在边长为 2 的等边△ABC 中,D 为 BC 的中点,E 是 AC 边上一点,则 BE+DE 的最小值为 . 4. 如图 4,钝角三角形 ABC 的面积为 9,最长边 AB=6,BD 平分∠ABC,点 M、N 分别是 BD、BC 上的动点,则 CM+MN 的最小值为 . 5. 如图 5,在△ABC 中,AM 平分∠BAC,点 D、E 分别为 AM、AB 上的动点,...