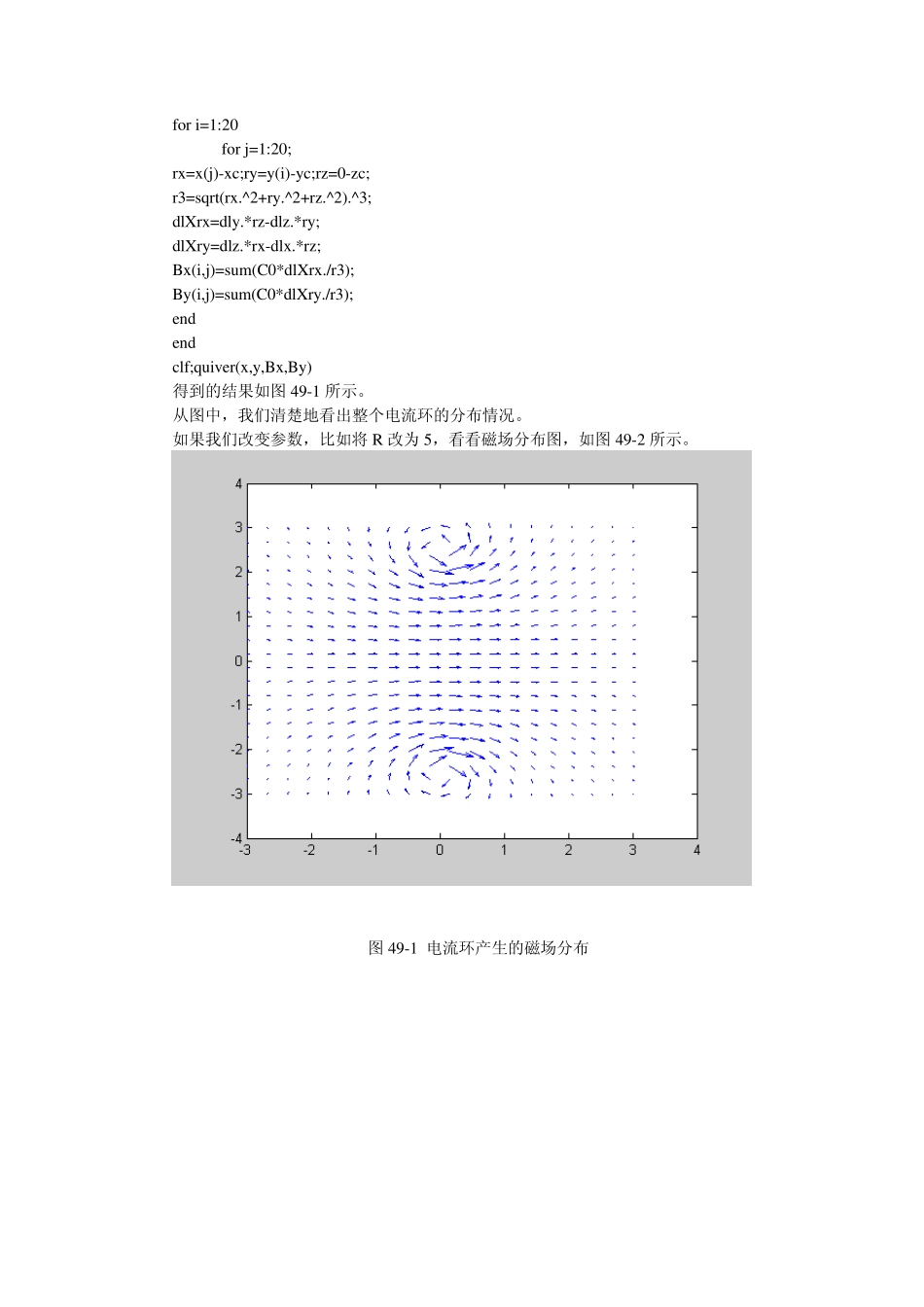
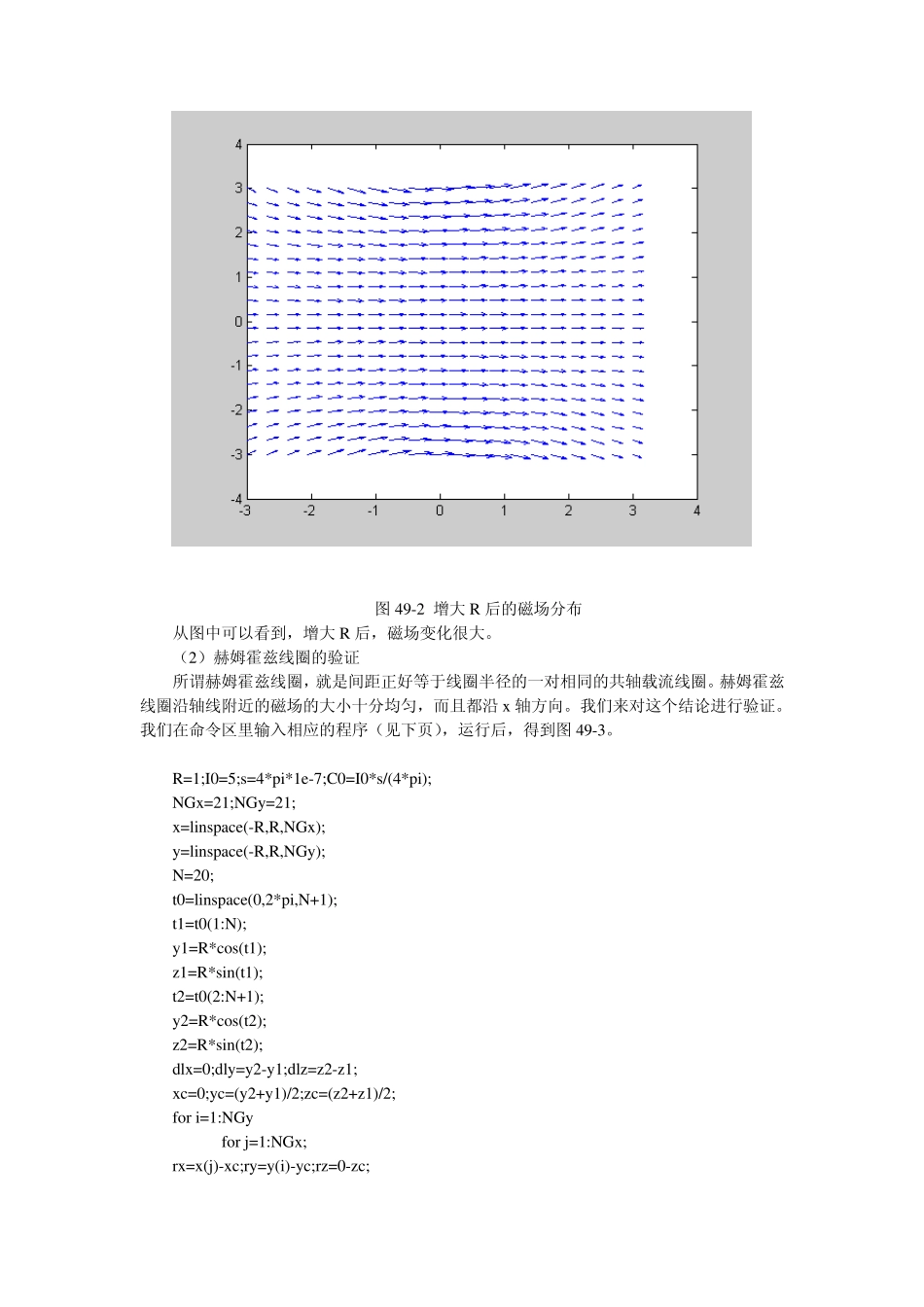
练习4 9 磁场计算 知识背景 磁场是一个很基本的电磁场现象。如同电场计算一样,磁场计算在科学研究和工程实际问题中有着广泛的应用。我们在这个练习中着手解决磁场问题。并试图用图形将数据可视化,从而使我们清楚地把握磁场特征。 主要内容 【本练习讲述知识点】 本练习考查读者综合使用编程、绘图、逻辑验证等来解决实际磁学问题的能力。我们将利用linspace语句、for循环语句、subplot和mesh绘图命令及逻辑运算符。练习中涉及到较为复杂的程序,希望读者仔细体会。 练习过程 (1)电流环产生的磁场 我们来结合实际例子看一下如何解决这类问题: 我们来看看如何用毕奥-萨伐定律计算电流环产生的磁场。磁学知识告诉我们,载流导线产生的磁场规律为: 任一电流元ldI在空间任一点P处产生的磁感应强度 Bd为: rrldIBd304 其中,r 为电流元到 P 点的矢径,dl 为导线圆的长度矢量。则 P 点的总磁场可沿载流导体全长积分各段产生的磁场来求得。 我们在命令区里输入: R=2.5;I0=4;s=4*pi*1e-7;C0=I0*s/(4*pi); x=linspace(-3,3,20);y=x; N=20; t0=linspace(0,2*pi,N+1); t1=t0(1:N); y1=R*cos(t1); z1=R*sin(t1); t2=t0(2:N+1); y2=R*cos(t2); z2=R*sin(t2); dlx=0;dly=y2-y1;dlz=z2-z1; xc=0;yc=(y2+y1)/2;zc=(z2+z1)/2; for i=1:20 for j=1:20; rx=x(j)-xc;ry=y(i)-yc;rz=0-zc; r3=sqrt(rx.^2+ry.^2+rz.^2).^3; dlXrx=dly.*rz-dlz.*ry; dlXry=dlz.*rx-dlx.*rz; Bx(i,j)=sum(C0*dlXrx./r3); By(i,j)=sum(C0*dlXry./r3); end end clf;quiver(x,y,Bx,By) 得到的结果如图49-1 所示。 从图中,我们清楚地看出整个电流环的分布情况。 如果我们改变参数,比如将 R 改为 5,看看磁场分布图,如图49-2 所示。 图49-1 电流环产生的磁场分布 图49-2 增大R 后的磁场分布 从图中可以看到,增大R 后,磁场变化很大。 (2)赫姆霍兹线圈的验证 所谓赫姆霍兹线圈,就是间距正好等于线圈半径的一对相同的共轴载流线圈。赫姆霍兹线圈沿轴线附近的磁场的大小十分均匀,而且都沿 x 轴方向。我们来对这个结论进行验证。我们在命令区里输入相应的程序(见下页),运行后,得到图49-3。 R=1;I0=5;s=4*pi*1e-7;C0=I0*s/(4*pi); NGx=21;NGy=21; x=linspace(-R,R,NGx); y=linspace(-R,R,NGy); N=20; t0=linspace(0,2*pi,N+1); t1=t0(1:N); y1=R*cos(t1); z1=R*sin(t1); t2=t...