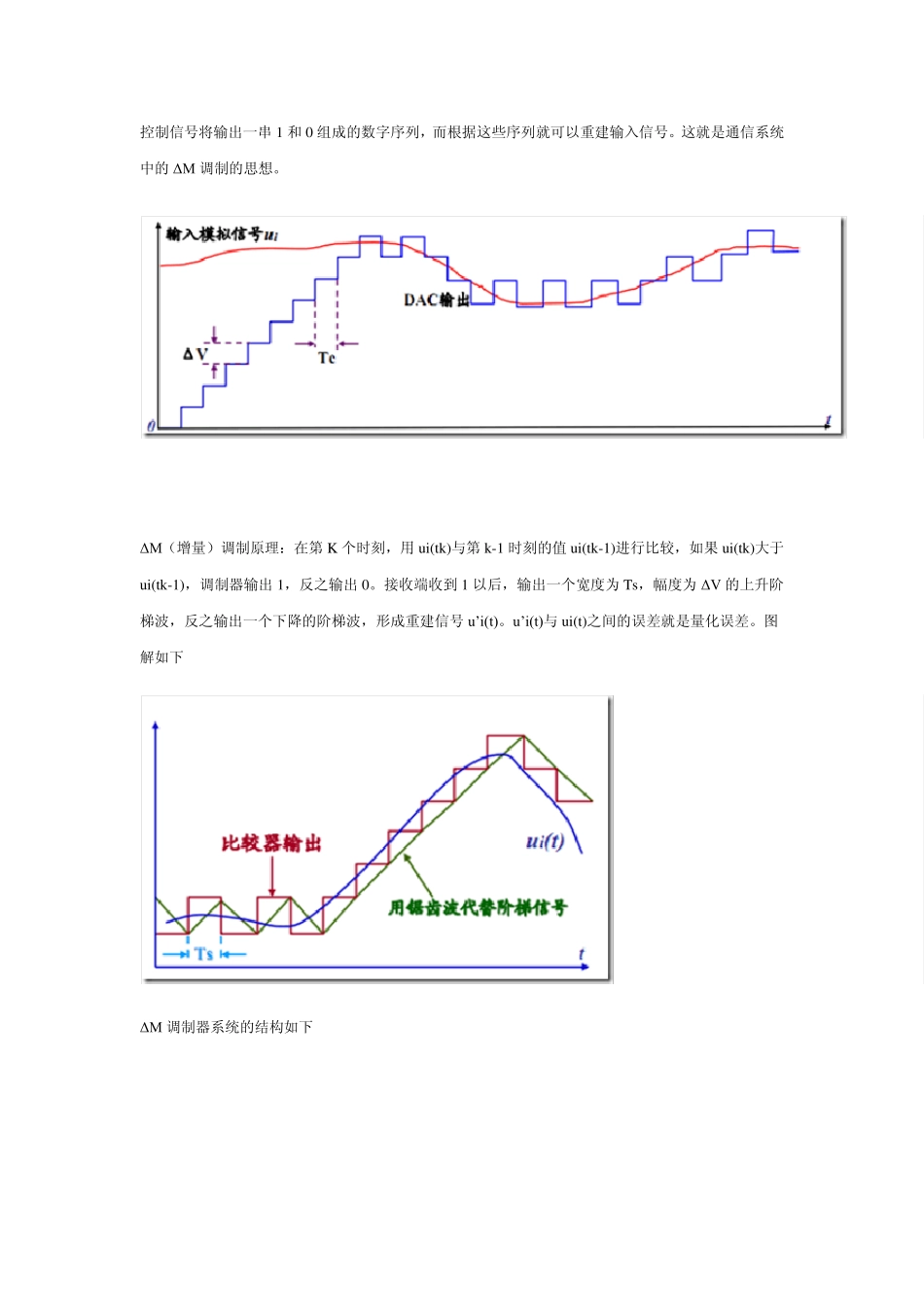
Σ-Δ调制型 ADC (2011-06-24 15:57:22) 转载 标签: 高通 量化噪声 噪声功率 输入信号 调制 分类: 学科知识 数字信号采集课上讲了一种感觉很牛逼的ADC,结合了N 中技术而成,能实现很高的采样精度,真是理论和实践的结合啊,想着不得不总结一下啊。 它是基于一个下面基本的公式开始的,信号量化噪声功率比的一般表达式为 SNqR(dB) = 6N + C 其中N 为 ADC 的分辨率。上式表明量化器的分辨率每增加一个比特,就可以获得6dB 的信噪比增益,而换个角度想,如果通过某种手段降低了量化噪声功率,不就相当于减少了量化器的量化分层数后而仍满足分辨率指标。而那种所谓的某种降低量化噪声功率的手段是什么呢? 就是过采样。为什么呢?因为量化噪声的特性指出,如果输入信号的最小幅度大于量化器的最小量阶,那么量化噪声总功率将是一个常数,而与采样频率Fs 无关,并在0~ Fs/2 的范围内均匀分布。而如果将采样频率提高,由于量化噪声与采样频率无关,量化噪声总功率不变,只是在更大的范围仍然呈均匀分布,如下图 所以得出的结论就是:过采样可以降低量化噪声功率! 然而仅仅是过采样,ADC 输出的数字信号仍然包含所有的量化噪声功率,而且数字信号数量也增加K倍。解决方法为使用数字滤波器对最高频率外的噪声滤波,然后再抽取。如下图 注意到采样频率远远大于 2fm(奈奎斯特频率),所以前面的抗混叠模拟低通滤波器可以省去,这是Σ-Δ 调制型 ADC 的一个优点。 采用过采样技术,可以在满足要求的SNqR 的情况下,减小量化去的分辨率N,相当于实现了“以速度换取分辨率” 的效果,但如果假想将分辨率降为 N=1,那将使采样频率升到极高的频率采样,显然这是不现实的。 这个问题主要涉及的就是一个 1bit的量化器,而这可以借鉴斜坡跟踪型 ADC 的改进型— — 随动跟踪型 ADC 来实现,这个可以参考下图来理解,斜坡跟踪型 ADC 中,DAC 输出一旦跟踪上输入信号,控制信号将输出一串1 和0 组成的数字序列,而根据这些序列就可以重建输入信号。这就是通信系统中的ΔM 调制的思想。 ΔM(增量)调制原理:在第 K 个时刻,用 u i(tk)与第 k-1 时刻的值 u i(tk-1)进行比较,如果 u i(tk)大于u i(tk-1),调制器输出1,反之输出0。接收端收到 1 以后,输出一个宽度为 Ts,幅度为 ΔV 的上升阶梯波,反之输出一个下降的阶梯波,形成重建信号u’i(t)。u’i(t)与 u i(t)之间的误差就是量化...