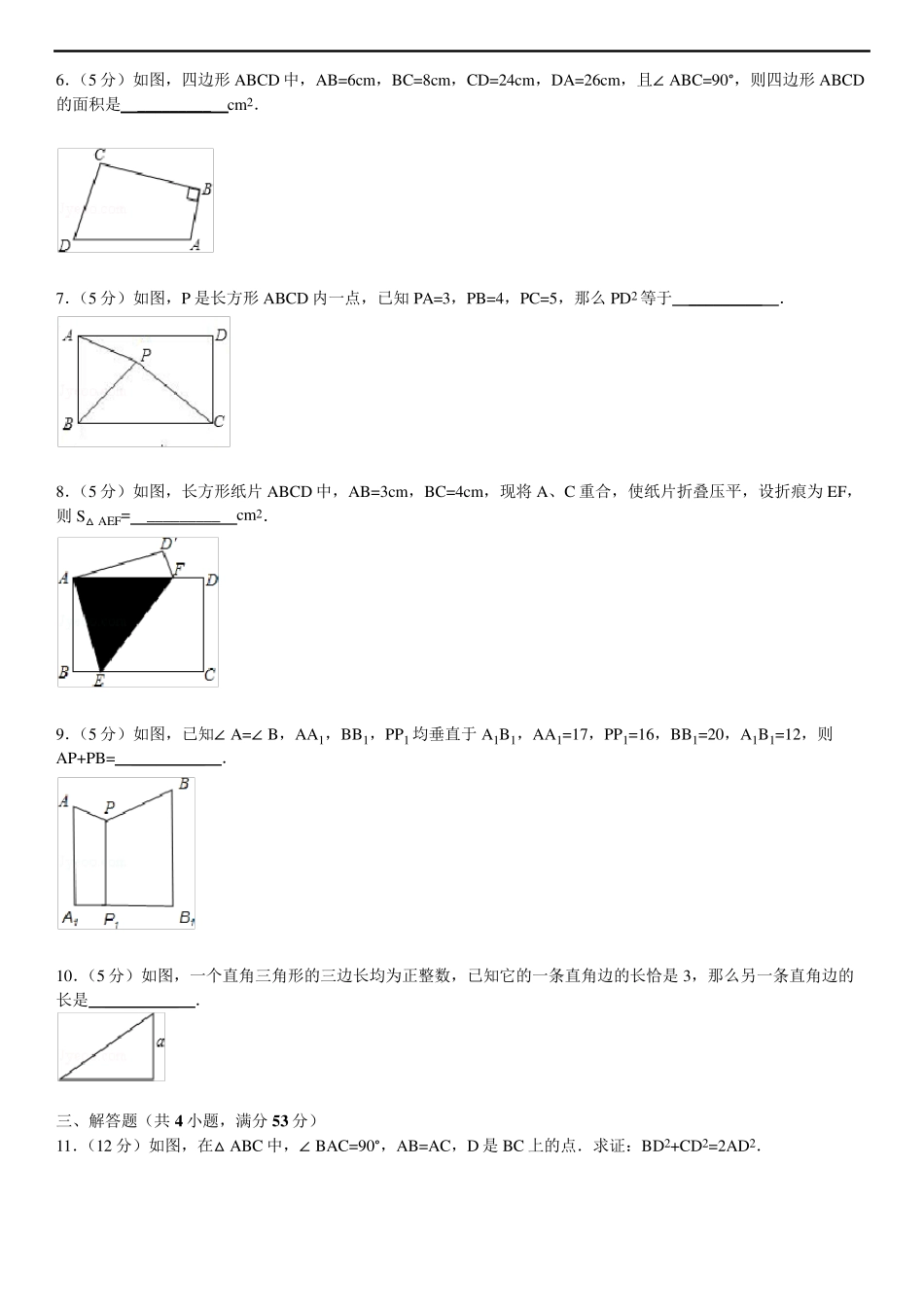
1 6 《勾股定理》拓展练习(含解析) 一、选择题(共 3 小题,每小题 4 分,满分 1 2 分) 1.(4 分)(1999•广西)如图,在四边形 ABCD 中,∠ A=60°,∠ B=∠ D=90°,BC=2,CD=3,则 AB=( ) A. 4 B. 5 C. 2 D. 2.(4 分)若三角形中的一条边是另一条边的 2 倍,且有一个角为 30°,则这个三角形是( ) A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 以上都不对 3.(4 分)如图,过△ABC 的顶点 A 的直线 DE∥ BC,∠ ABC、∠ ACB 的平分线分别交 DE 于 E、D 两点,若AB=6,AC=8,则 DE=( ) A. 10 B. 14 C. 16 D. 24 二、填空题(共 7 小题,每小题 5 分,满分 3 5 分) 4.(5 分)如图,P 为△ABC 边 BC 上的一点,且 PC=2PB,已知∠ ABC=45°,∠ APC=60°,则∠ ACB 的度数是 _________ °. 5.(5 分)(1997•陕西)如图,在四边形 ABCD 中,AB:BC:CD:DA=2:2:3:1,且∠ ABC=90°,则∠ DAB的度数是 _________ °. 6.(5 分)如图,四边形ABCD 中,AB=6cm ,BC=8cm ,CD=24cm ,DA=26cm ,且∠ ABC=90° ,则四边形ABCD的面积是 _________ cm 2. 7.(5 分)如图,P 是长方形ABCD 内一点,已知PA=3,PB=4,PC=5,那么PD2等于 _________ . 8.(5 分)如图,长方形纸片ABCD 中,AB=3cm ,BC=4cm ,现将A、C 重合,使纸片折叠压平,设折痕为 EF,则S△AEF= _________ cm 2. 9.(5 分)如图,已知∠ A=∠ B,AA1,BB1,PP1均垂直于A1B1,AA1=17,PP1=16,BB1=20,A1B1=12,则AP+PB= _________ . 10.(5 分)如图,一个直角三角形的三边长均为正整数,已知它的一条直角边的长恰是3,那么另一条直角边的长是 _________ . 三、解答题(共 4 小题,满分53 分) 11.(12 分)如图,在△ABC 中,∠ BAC=90° ,AB=AC,D 是BC 上的点.求证:BD2+CD2=2AD2. 12.(13 分)如图:在△ABC 中,AB=BC=AC,AE=CD,AD 与BE 相交于点P,BQ⊥AD 于Q. 求证:①△ADC≌ △ BEA; ② BP=2PQ. 13.(14 分)如图,在等腰直角△ABC 的斜边上取异于B,C 的两点E,F,使∠ EAF=45°,求证:以EF,BE,CF 为边的三角形是直角三角形. 14.(14 分)如图,在Rt△ABC 中,∠ A=90°,D 为斜边BC 中点,DE⊥DF,求证:EF2=BE2+CF2. 《第1 章 勾股...