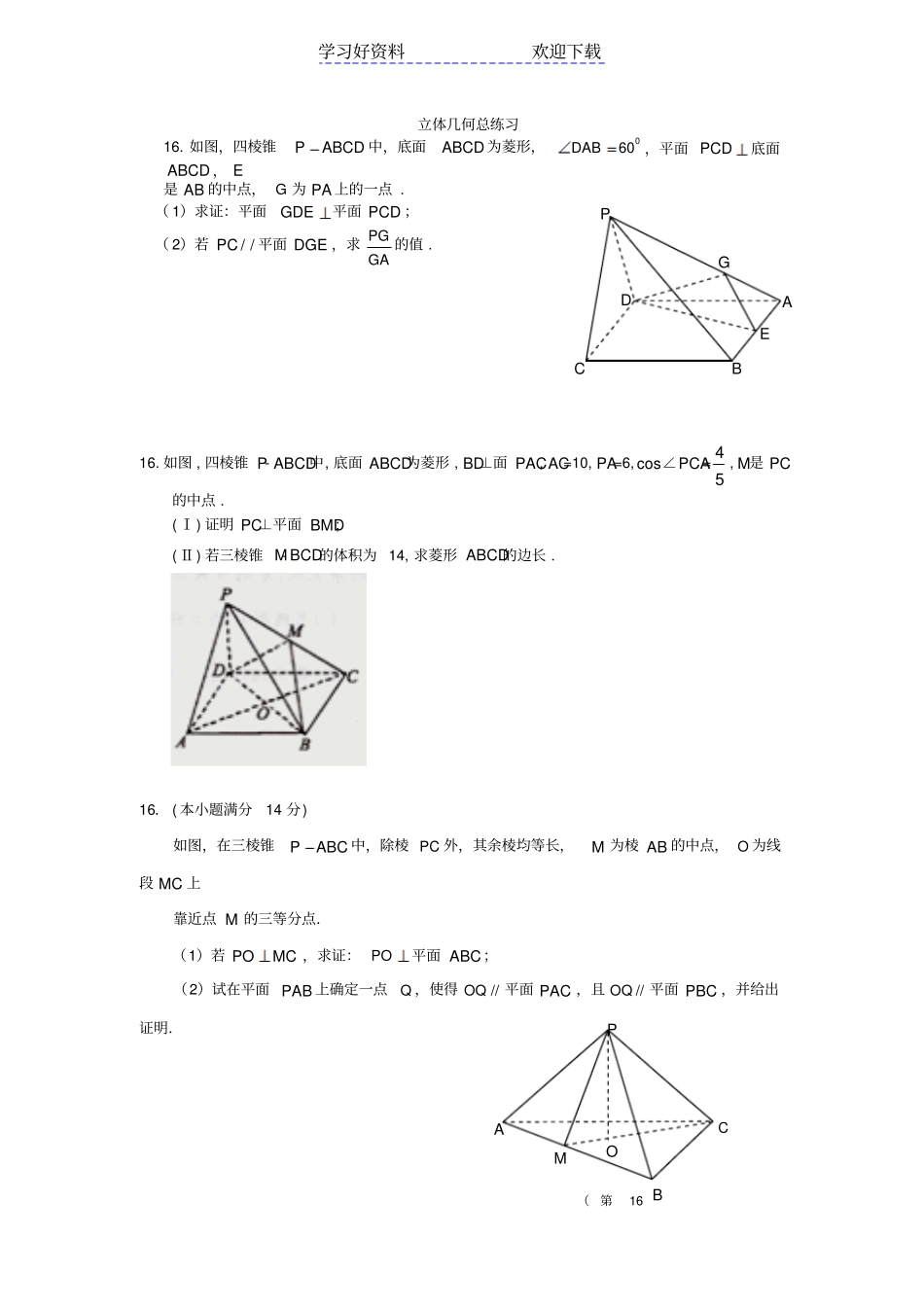
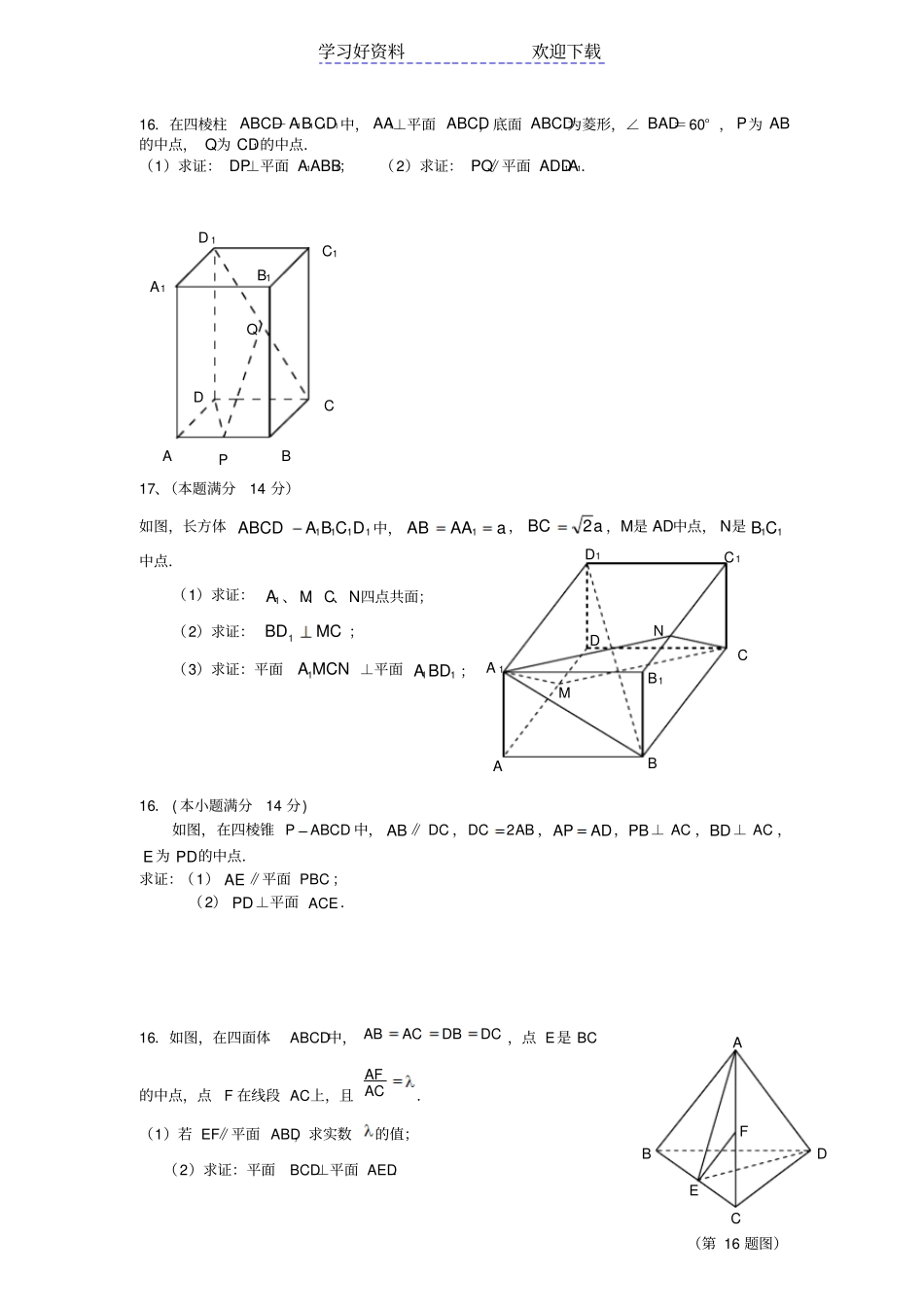
学习好资料欢迎下载PABCOM(第16立体几何总练习16. 如图,四棱锥PABCD 中,底面ABCD 为菱形,060DAB,平面 PCD底面ABCD , E是 AB 的中点, G 为 PA 上的一点 . ( 1)求证:平面GDE平面 PCD ;( 2)若/ /PC平面 DGE ,求 PGGA的值 .16. 如图 , 四棱锥 P- ABCD中, 底面 ABCD为菱形 , BD⊥面 PAC, AC=10, PA=6, cos∠PCA= 45, M是 PC的中点 . ( Ⅰ) 证明 PC⊥平面 BMD; ( Ⅱ) 若三棱锥 M- BCD的体积为 14, 求菱形 ABCD的边长 . 16. ( 本小题满分14 分) 如图,在三棱锥PABC 中,除棱 PC 外,其余棱均等长,M 为棱 AB 的中点, O 为线段 MC 上靠近点 M 的三等分点.(1)若 POMC ,求证: PO平面 ABC;(2)试在平面 PAB 上确定一点Q ,使得//OQ平面 PAC ,且//OQ平面 PBC ,并给出证明.PABCDEG学习好资料欢迎下载15 ( 14分 ) . 如 图 , 在 长 方 体1111ABCDA B C D中 , 点 E 在 棱1CC 的 延 长 线 上 , 且11112CCC EBCAB. ( Ⅰ) 求证 :1D E ∥平面1ACB ; ( Ⅱ) 求证 : 平面11D B E平面1DCB ; ( Ⅲ) 求四面体11D B AC 的体积 . 16. 、如图,已知 E , F 分别是正方形ABCD 边 BC 、 CD 的中点, EF 与 AC 交于点 O ,PA 、 NC 都垂直于平面ABCD ,且4PAAB,2NC, M 是线段 PA 上一动点.(Ⅰ)求证: 平面 PAC平面 NEF ;(Ⅱ)若//PC平面 MEF ,试求:PMMA 的值;B E A D C 1A1B1C1D第 16 题图学习好资料欢迎下载16.在四棱柱ABCD-A1B1C1D1中, AA1⊥平面 ABCD,底面 ABCD为菱形,∠ BAD=60° , P为 AB的中点, Q为 CD1 的中点.(1)求证: DP⊥平面 A1ABB1;(2)求证: PQ∥平面 ADD1A1.17、(本题满分14 分)如图,长方体1111DCBAABCD中,aAAAB1,aBC2,M是 AD中点, N是11CB中点.(1)求证:1A 、 M、C、N四点共面;(2)求证:MCBD1;(3)求证:平面MCNA1⊥平面11BDA;16. ( 本小题满分14 分) 如图,在四棱锥 PABCD 中, AB∥ DC ,2DCAB ,APAD,PB⊥ AC ,BD⊥ AC ,E 为 PD的中点.求证:(1) AE ∥平面 PBC ;(2) PD⊥平面 ACE.16.如图,在四面体ABCD中, ABACDBDC ,点 E是 BC 的中点,点F 在线段 AC上,且AFAC.(1)若 EF∥平面 ABD,求实数的值;(2)求证:平面BCD⊥平面 AED.B1 A B C D QPA1 C1 D 1 A B C D A 1B1C1D1M N (第 16 题图)E A B C D F 学习好资料欢迎下载