复合闭路定理VIP免费

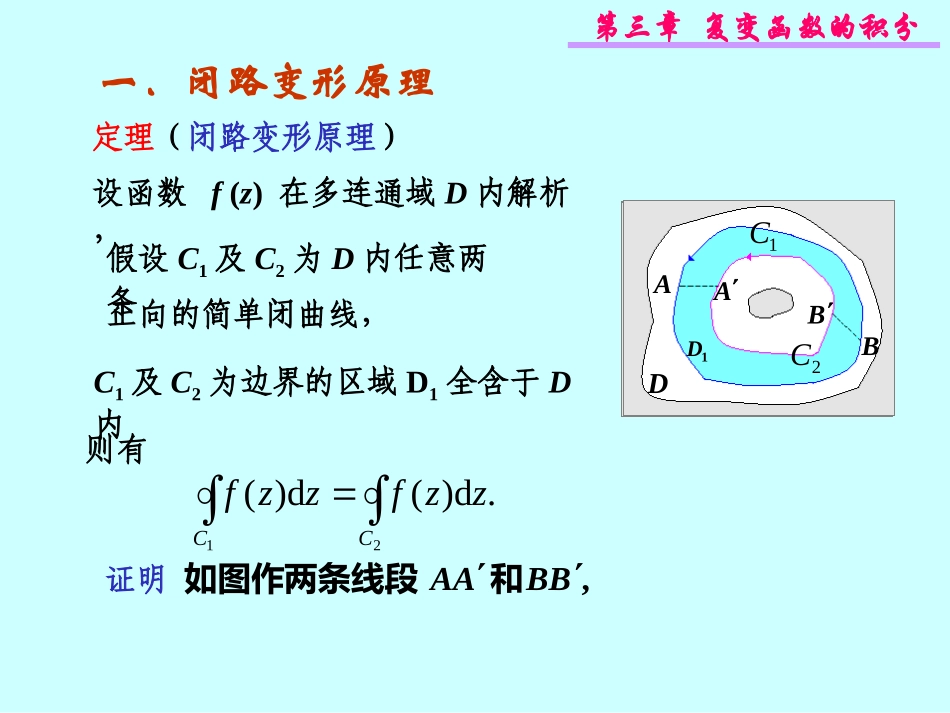
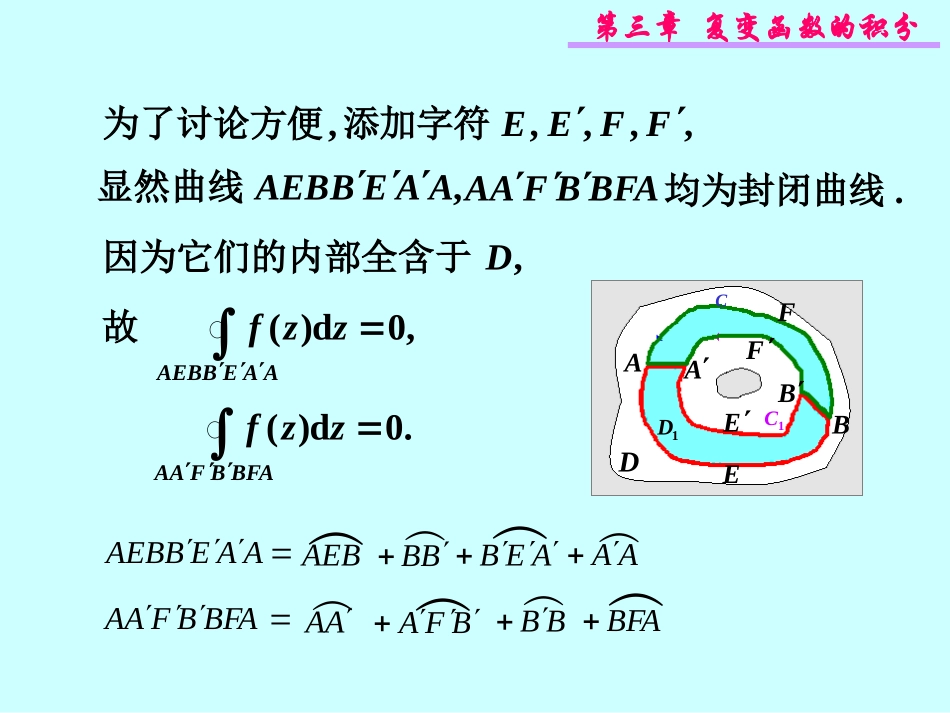
第三节复合闭路定理•一．闭路变形原理•二．复合闭路定理,BBAA和证明：如图作两条线段定理（闭路变形原理）D1C2C1DABB.d)(d)(21CCzzfzzf设函数f(z)在多连通域D内解析，假设C1及C2为D内任意两条正向的简单闭曲线，C1及C2为边界的区域D1全含于D内则有证明A一．闭路变形原理第三章复变函数的积分DC1C1DAABBEEFF,AAEBAEB显然曲线BFABFAA,,,,,FFEE添加字符为了讨论方便.均为封闭曲线,D因为它们的内部全含于,0d)(AAEBAEBzzf故.0d)(BFABFAAzzfAAEBAEB︵AEB︵BB︵AEB︵AABFABFAA︵AA︵BFA︵BB︵BFA第三章复变函数的积分AAEBAEBzzfd)(由,0d)(BFABFAAzzf得D1C2C1DAABBEEFF,0d)(d)(21CCzzfzzf即.d)(d)(21CCzzfzzf有此式说明：解析函数沿闭曲线的积分,不因闭曲线在区域内作连续变形而改变它的值.1d)(Czzf2d)(CzzfAAzzfd)(︵AAzzfd)(︵,0d)(BBzzf︵BBzzfd)(︵第三章复变函数的积分由本章第一节例4知,42d11zizz将基本定理推广到多连连通域中.因为|z|=4是包含z=-1在内的闭曲线，0002)(10nnizzdzCn.2)(idzzf根据闭路变形原理，简单闭曲线Γ都有4.d11zzz例1计算对于包含z0的任何一条正向第三章复变函数的积分Cdzzz01,2iz0在C的内部z0在C的外部,0DC1C2C3CnC定理(复合闭路定理)设C为多连通域D内的一条简单闭曲线，C1,C2,…,Cn是在C内部的简单闭曲线，它们互不包含也互不相交，并且以C1,C2,…,Cn为边界的区域全含于D，如果f(z)在D内解析，则.)()()2(1niccidzzfdzzf其中C,C1,C2,…,Cn为均取逆时针方向.,0)()1(dzzf其中Γ为C及Ck（k=1,2,…,n)所围成的复合闭路（C取逆时针方向，Ck取顺时针方向）.二．复合闭路定理第三章复变函数的积分解C例2C是正向简单闭曲线，包含|z|=2在内，求Czzzzd2)1(22-2xyo在C内部作两个互不包含也互不相交的正向圆周C1和C2,1CC1只包含奇点0,2CC2只包含奇点-2.Czzzzd2)1(221d2)1(22Czzzz据复合闭路定理有2d2)1(22Czzzz显然函数在复平面有两个奇点0和-2,zzzzf2)1(2)(2第三章复变函数的积分zzz2)1(22)2()1(2zzz211zz1d21Czz1d1Czz2d21Czz2d1Czz.4i=0+2πi+2πi+0第四节柯西积分公式•一．柯西积分公式•二．举例设B为一单连通域，0)(zzzf则函数在z0不解析，如果f(z)在B内解析，所以在B内沿围绕z0的一条闭曲线C的积分一般不为零.Cdzzzzf0)(又根据闭路变形原理，这积分的值沿任何一条围绕z0的简单闭曲线都是相同的.则取以z0为中心，作为积分曲线C.由于f(z)的连续性，在C上的函数f(z)的值将随着δ的缩小而逐渐接近于它在圆心z0处的值.即Cdzzzzf00)(Cdzzzzf001)(.)(20zifCdzzzzf0)(z0为B内一点，δ为半径的很小的正向圆周|z-z0|<δ第三章复变函数的积分一．柯西积分公式)(2)(00zifdzzzzfC定理如果f(z)在区域D内解析，C为D内任意一条正向简单闭曲线，它的内部完全含于D，z0为C内任意一点，则有柯西积分公式注：（1）如果f(z)在有界闭区域D上解析，公式仍成立.（2）有界闭区域上的解析函数，它在区域内任一点所取的值可以用它在边界上的值表示出来.（3）柯西公式是解析函数的最基本的性质之一，可以帮助我们研究解析函数的许多重要性质.第三章复变函数的积分上连续，则在RzzC|:|021)(0zf200)Re(dzfi内解析，RzzC|:|0设f(z)在一个解析函数在圆心处的值等于它在圆周上的200Re)Re(21dRiezfiiii200)Re(21dzfi,Re:0izzC因为证明Cdzzzzfizf00)(21)(dRiedzi平均值.说明：推论1平均值公式第三章复变函数的积分推论2设f(z)在由简单闭曲线C1,C2围成的二连通区域D内1C00)(21)(zdzzzfπizf内解析，并在曲线C1,C2上连续，C2在C1的内部，z0为D内一点，则2C0)(21zdzzzfπiC1C2D或πizfzdzzzfzdzzzf2)()()(0C0C021...