平行轴定理及垂直轴定理VIP免费

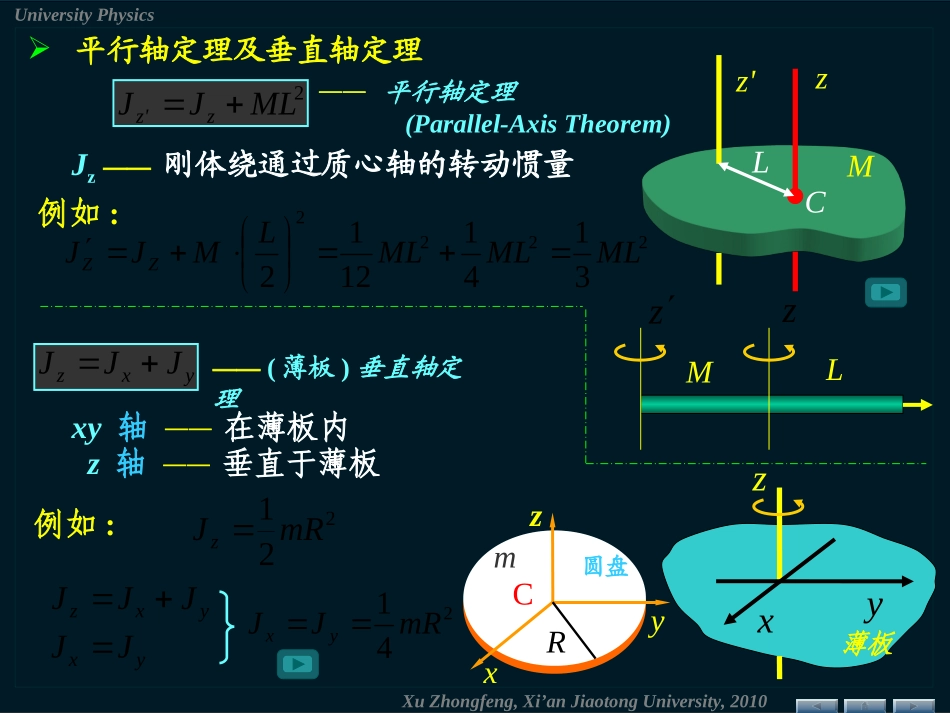
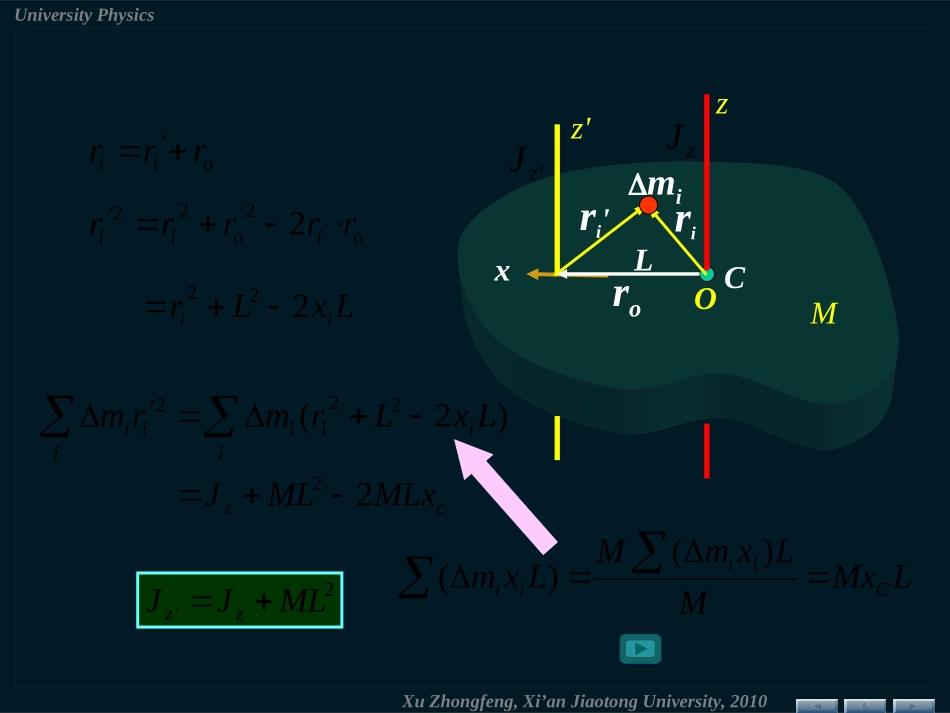
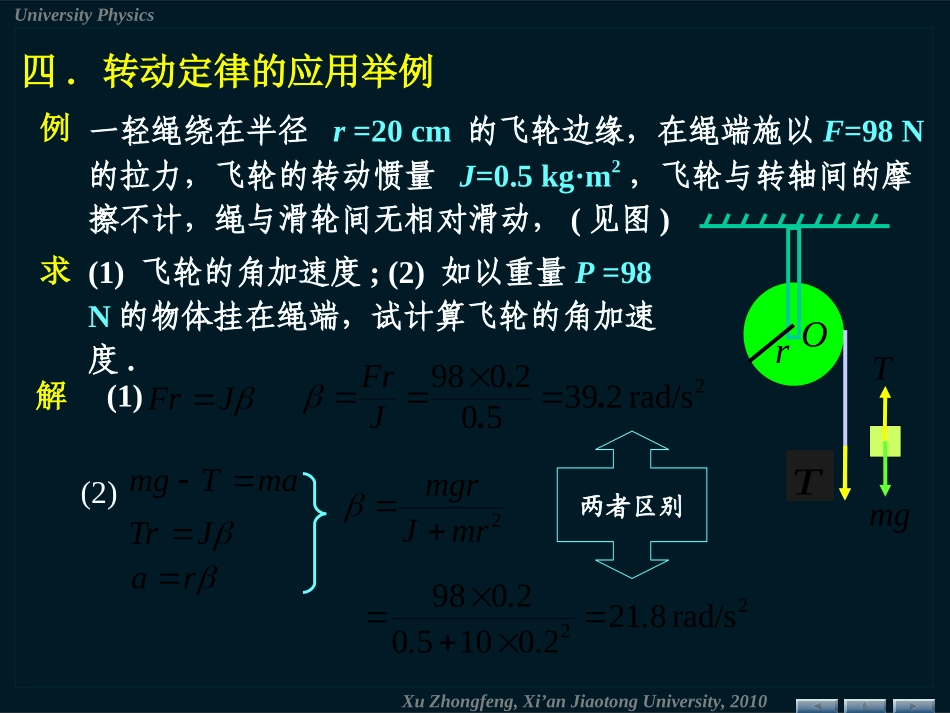
XuZhongfeng,Xi’anJiaotongUniversity,2010UniversityPhysics平行轴定理及垂直轴定理zLCMz'2MLJJz'zJz——刚体绕通过质心轴的转动惯量例如:zMLz222231411212MLMLMLLMJJZZ——平行轴定理(Parallel-AxisTheorem)zxy薄板yxzJJJ——(薄板)垂直轴定理xy轴——在薄板内z轴——垂直于薄板例如:yxz圆盘RCm221mRJzyxzJJJyxJJ241mRJJyxXuZhongfeng,Xi’anJiaotongUniversity,2010UniversityPhysicsCzMzJz''zJroriri'Loiirrrmioioiirrrrr2222LxLrii222x)2(222LxLrmrmiiiiiiiczMLxMLJ222'MLJJzzOLMxMLxmMLxmCiiii)()(XuZhongfeng,Xi’anJiaotongUniversity,2010UniversityPhysics四.转动定律的应用举例FOr(1)飞轮的角加速度;(2)如以重量P=98N的物体挂在绳端，试计算飞轮的角加速度.解(1)JFr2rad/s239502098...JFrmaTmg(2)JTrra两者区别gmT例求一轻绳绕在半径r=20cm的飞轮边缘，在绳端施以F=98N的拉力，飞轮的转动惯量J=0.5kg·m2，飞轮与转轴间的摩擦不计，绳与滑轮间无相对滑动，(见图)2mrJmgr22rad/s8212010502098....TXuZhongfeng,Xi’anJiaotongUniversity,2010UniversityPhysics一根长为l，质量为m的均匀细直棒，可绕轴O在竖直平面内转动（光滑无摩擦），初始时它在水平位置求它由此下摆角时的和OlmCx解mxggmxMzdd取一质元CmxmxdCzmgxM重力对整个棒的合力矩等于重力全部集中于质心所产生的力矩dmcos21mglMzlgmlmglJMz2cos33cos212gm例lgt2cos3ddddθωlg00d2cos3dlgsin3XuZhongfeng,Xi’anJiaotongUniversity,2010UniversityPhysics匀质圆盘以0在水平桌面上转动,受摩擦力而静止解rrsmd2πddmgrfrMzdddRzzMM0d例求到圆盘静止所需时间取一质元摩擦力矩RmgRrrgR32d202tJMzddtmRmgRdd21322d43d000gRttgRt430由转动定律Rg34tRgt340tRg34022132mRmgRXuZhongfeng,Xi’anJiaotongUniversity,2010UniversityPhysics例一个刚体系统，如图所示，已知，转动惯量231mlJ，现有一水平力作用于距轴为l'处求轴对棒的作用力（也称轴反力）。解设轴对棒的作用力为NyxNN,JFl'由质心运动定理2lmmaNFcxx022lmmamgNcyy)12'3('2llFFJFlmlNxmgNyl'l320xN打击中心质心运动定理与转动定律联用xNyNOCgm'lF质点系由转动定律XuZhongfeng,Xi’anJiaotongUniversity,2010UniversityPhysics§6.2绕定轴转动刚体的动能动能定理一.转动动能zOirivimP•Nimmmm,......,,.......,,21NiNirrrrvvvv,...,,...,,...,,...,,21,21221iikimEv2221iirm)21(22iikirmE刚体对定轴的总动能为2221iirm221JEk,其动能为F'rrdd设系统包括有N个质量元取第i个质元定轴转动刚体的动能等于转动惯量与其角速度平方乘积的一半结论转动物体具有储能、稳速等作用：……各质元速度不同，但角速度相同二.力矩的功sFAdcosddrFdcosFrdrFdMXuZhongfeng,Xi’anJiaotongUniversity,2010UniversityPhysicsddMA(力矩的功就是力的功)对一有限过程21dMA若M=C)(12MA(积分形式）(2)内力矩作功之和为零。讨论(1)合力矩的功iiiiiiAMMMA212121d)d(d三.转动动能定理——合力矩功的效果kEJd)21d(2ddMAd)ddd(JtJ对于一有限过程2121)21d(d2JAA21222121JJkE绕定轴转动刚体在任一过程中动能的增量，等于在该过程中作用在刚体上所有外力所作功的总和。——动能定理XuZhongfeng,Xi’anJiaotongUniversity,2010UniversityPhysics刚体的机械能pkEEE刚体重力势能CmghJE221iipghmECiimg...