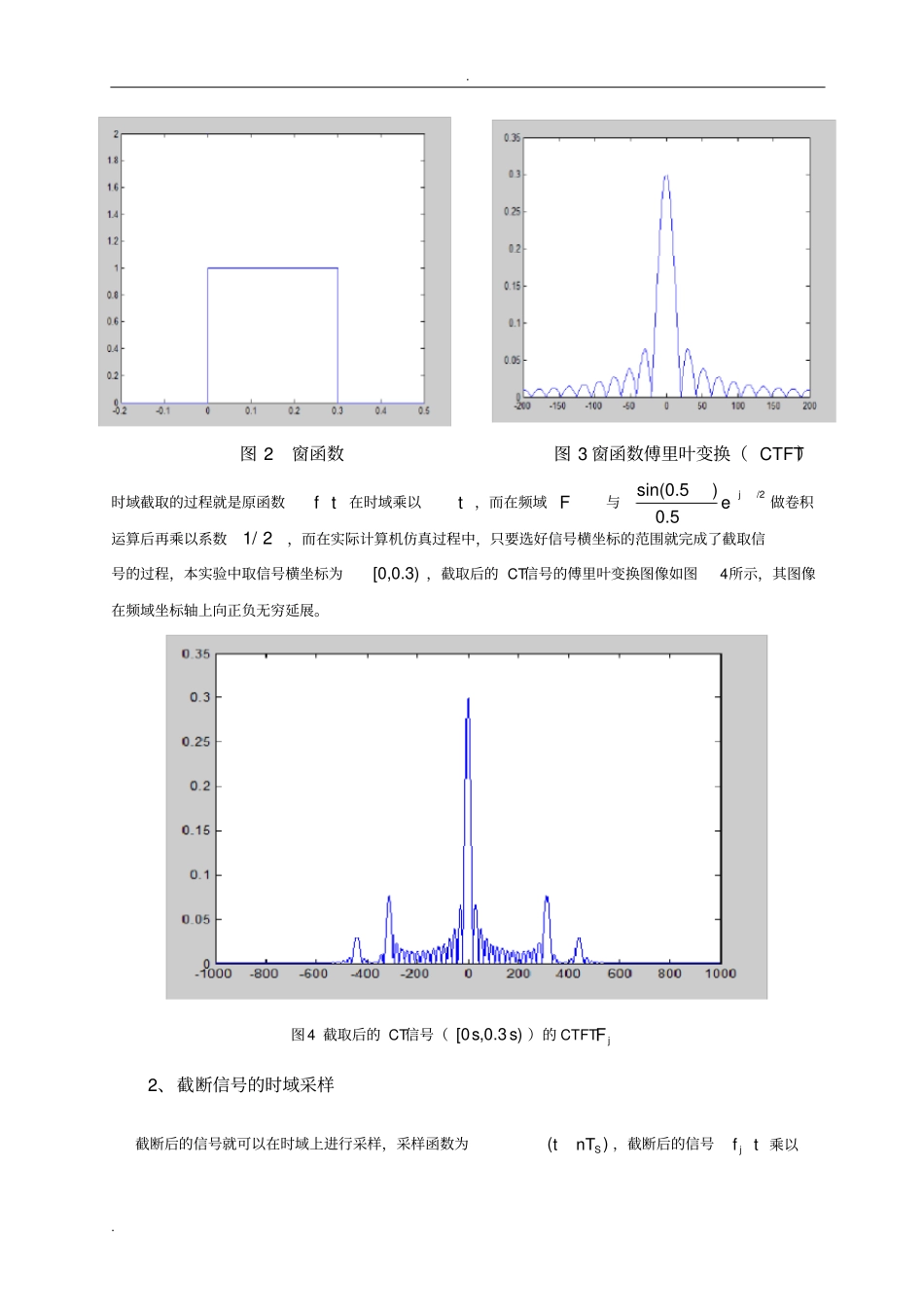
. . 信号采样与恢复过程中的混叠及其滤波一、实验目的:(1)理解连续时间信号的采样与恢复过程;(2)掌握采样序列的频域分析和滤波,信号的恢复,掌握Shannon采样定理;(3)学会利用 MATLAB软件分析信号采样、滤波与恢复的过程。(4)学会 FIR 滤波器的简单设计方法二、实验内容:给定原始信号如下式所示:12( )10.5sin 20.2sin 2f tf tf t ,其中,12,ff 是信号原始频率(本实验中为自选常数,1f 为低频,2f 为高频)。确定一个采样频率sf 对( )f t 进行采样,再将采样得到的序列进行DFT,画出过程中各信号的图形。进行频域高、低频滤波,再反变换得出处理后恢复出来的信号。将实验过程中得到的图形与理论图形进行比较,发现不同点并加以解释。三、实验过程:先选定 f1=50hz 、270fHz ,则原始信号表示为:( )10.5sin(250 )0.2sin(270 )f ttt1、原信号时域截取:因为在计算机中只能计算离散的点列,若要用 MATLAB处理图形, 只能先对信号进行截取和采样。 本实验选定矩形截取窗口的宽度为原信号周期的m倍,m为正整数。 所以画出截取后的信号图像为. . 图 1 截断后的信号图像原信号中低频为 50Hz,高频为 70Hz,取采样频率sf 为3倍的2f ,即370210fsHzHz 。50和70的最大公约数为 10,所以原信号的最小正周期为1/10s ,这里取 m为3(即取窗口函数的宽度为 3/10s ),相应的采样点数=1400.342Nc,所以窗口函数为100.30tst其他其图像如图 2所示, 其傅立叶变换图像如图3所示,其公式如下:/2sin(0.5)0.5jFte,其中0.3s. . 图 2 窗函数图 3 窗函数傅里叶变换( CTFT)时域截取的过程就是原函数f t在时域乘以t ,而在频域 F与/2sin(0.5)0.5je做卷积运算后再乘以系数1/ 2,而在实际计算机仿真过程中,只要选好信号横坐标的范围就完成了截取信号的过程,本实验中取信号横坐标为[0,0.3) ,截取后的 CT信号的傅里叶变换图像如图4所示,其图像在频域坐标轴上向正负无穷延展。图4 截取后的 CT信号( [0 ,0.3 )ss )的 CTFTjF2、截断信号的时域采样截断后的信号就可以在时域上进行采样,采样函数为()StnT,截断后的信号jft 乘以. . ()SnnT,所以在频域相当于1/ 2jF与()ssn进行卷积, 其得到的图像为周期的,其图像与离散采样信号的DTFT形式相同。以上为 CT信号的分析,对于离散信号,为了适应计算机的处理方式,我们需要采用DFT和IDFT进行计算求解。采样后的离散信号图像为下图所...