双侧检验和单侧检验VIP免费

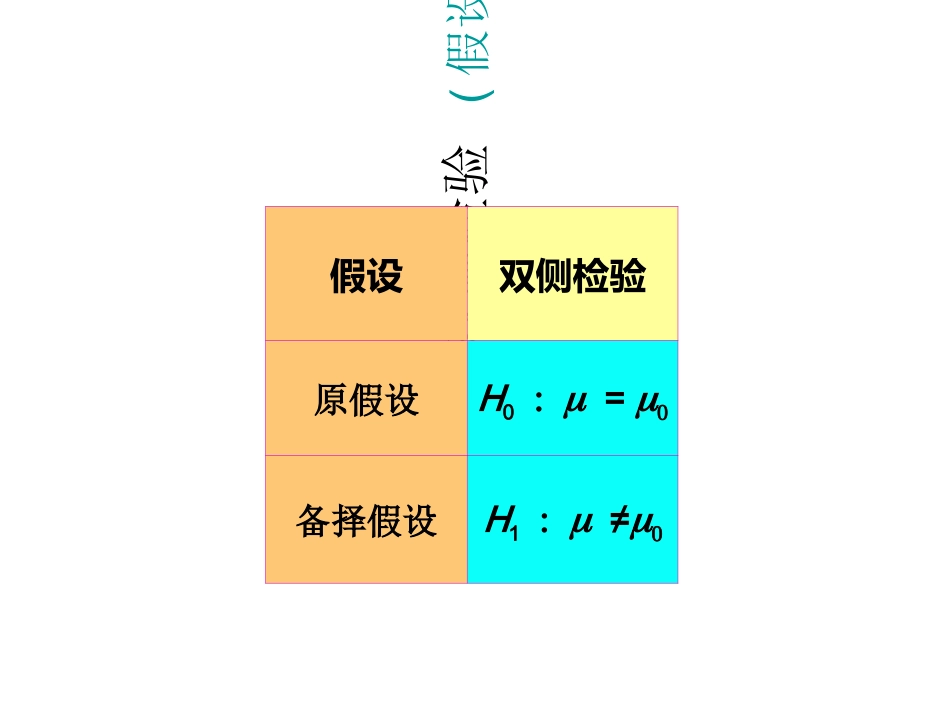
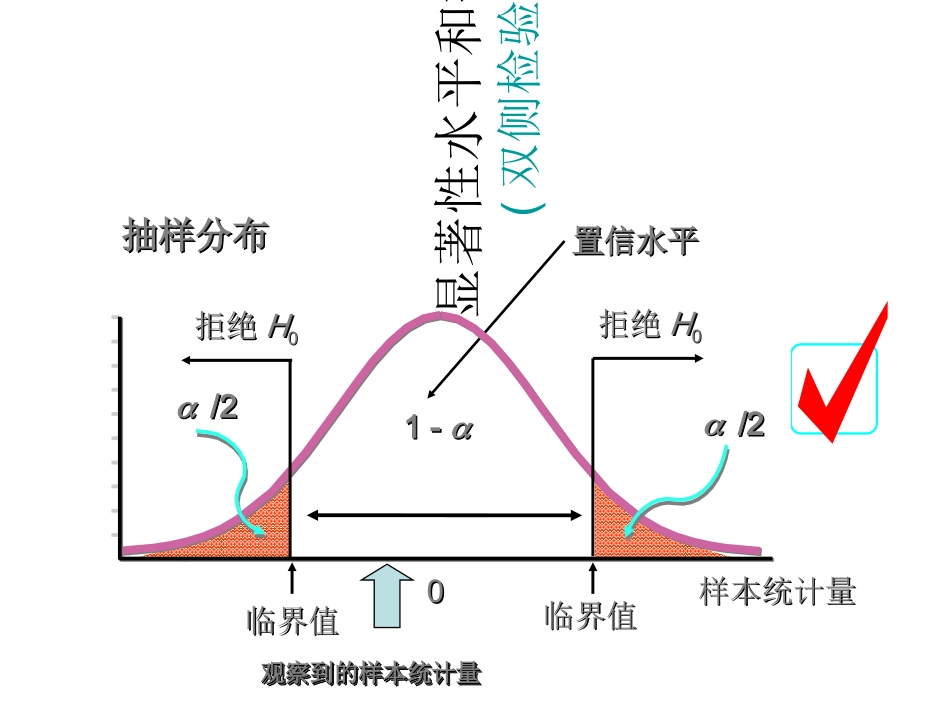
假设检验上机教程•1、单样本t检验•2、独立样本t检验•3、配对样本t检验双侧检验(假设的形式)假设双侧检验原假设H0=备择假设H1≠显著性水平和拒绝域(双侧检验)00临界值临界值临界值临界值/2/2/2/2样本统计量样本统计量拒绝拒绝HH00拒绝拒绝HH00抽样分布抽样分布1-1-置信水平置信水平观察到的样本统计量观察到的样本统计量观察到的样本统计量观察到的样本统计量决策规则1.给定显著性水平，，，，，，，，，，，z，z，t，t2.将检验统计量的值与，，，，，，，，，，3.作出决策–双侧检验：I统计量I临界值，拒绝H0–左侧检验：统计量-临界值，拒绝H0–右侧检验：统计量临界值，拒绝H0双侧检验的P值//22//22ZZ拒绝拒绝HH00拒绝拒绝HH000000临界值临界值临界值临界值计算出的样本统计量计算出的样本统计量计算出的样本统计量计算出的样本统计量计算出的样本统计量计算出的样本统计量计算出的样本统计量计算出的样本统计量临界值临界值临界值临界值1/21/2PP值值1/21/2PP值值1/21/2PP值值1/21/2PP值值(P-value)1.在原假设为真的条件下，检验统计量的观察值大于或等于其计算值的概率–双侧检验为分布中两侧面积的总和2.P越小表明拒绝H0的理由愈充分3.P可认为是，拒绝了不应该拒绝的原假设的风险值，这个值越小，表明犯错的风险越小，被称为观察到的(或实测的)显著性水平4.决策规则：若p值,拒绝H0P检验的规则•对一给定的样本，P值越小，犯第一类错误的概率也越小，如果P小于或者等于可接受的最大第一类错误风险a，则拒绝原假设；相反，如果P大于a，则认为第一类错误的风险太大了，于是不拒绝原假设。总体均值的检验（单一样本检验方法的总结）假设双侧检验左侧检验右侧检验假设形式H0，=H1，H0，H1，<H0，H1，>统计量未知：拒绝域P值决策拒绝H0nsxt0)1(2/ntt)1(ntt)1(nttP，，，，已知的拒绝域同大样本已知的拒绝域同大样本/2,/2,[]xxXStXSt两个总体均值之差的检验(12，22未知且不相等1222)1.假定条件–两个总体都是正态分布，12，22未知且不相等，即1222–样本容量不相等，即n1n22.检验统计量自由度：自由度：自由度：自由度：2221212121)()()(nsnsxxvt1122222121212222121nnsnnsnsnsv两个总体均值之差的检验(12，22未知且不相等1222)1.假定条件–两个总体都是正态分布，12，22未知且不相等，即1222–样本容量相等，即n1=n2=n2.检验统计量nssxxnsnsxxt222121212221212121)()()()()1(2221nnn自由度：自由度：自由度：自由度：两个总体均值之差的检验(12，22未知但12=22)1.1.假定假定条件条件两个独立的小样本两个独立的小样本两个总体都是正态分布两个总体都是正态分布1122、、2222未知但相等，即未知但相等，即1122==22222.2.检验检验统计量统计量21212111)()(nnsxxtp其中：其中：其中：其中：2)1()1(212222112nnsnsnsp221nn自由度：自由度：自由度：自由度：两个总体均值之差的检验(匹配样本)1.假定条件–两个总体配对差值构成的总体服从正态分布–配对差是由差值总体中随机抽取的–数据配对或匹配(重复测量(前/后))2.检验统计量)1(~0ntnsddtdd样本差值均值样本差值均值样本差值标准差样本差值标准差dniindd11)(12dniidndds两个总体均值之差的检验(匹配样本检验方法的总结)假设双侧检验左侧检验右侧检验假设形式H0，d=0H1：d0H0：d0H1：d<0H0：d0H1：d>0统计量拒绝域P值决策拒绝H0)1(2/ntt)1(ntt)1(nttPddnsddt0