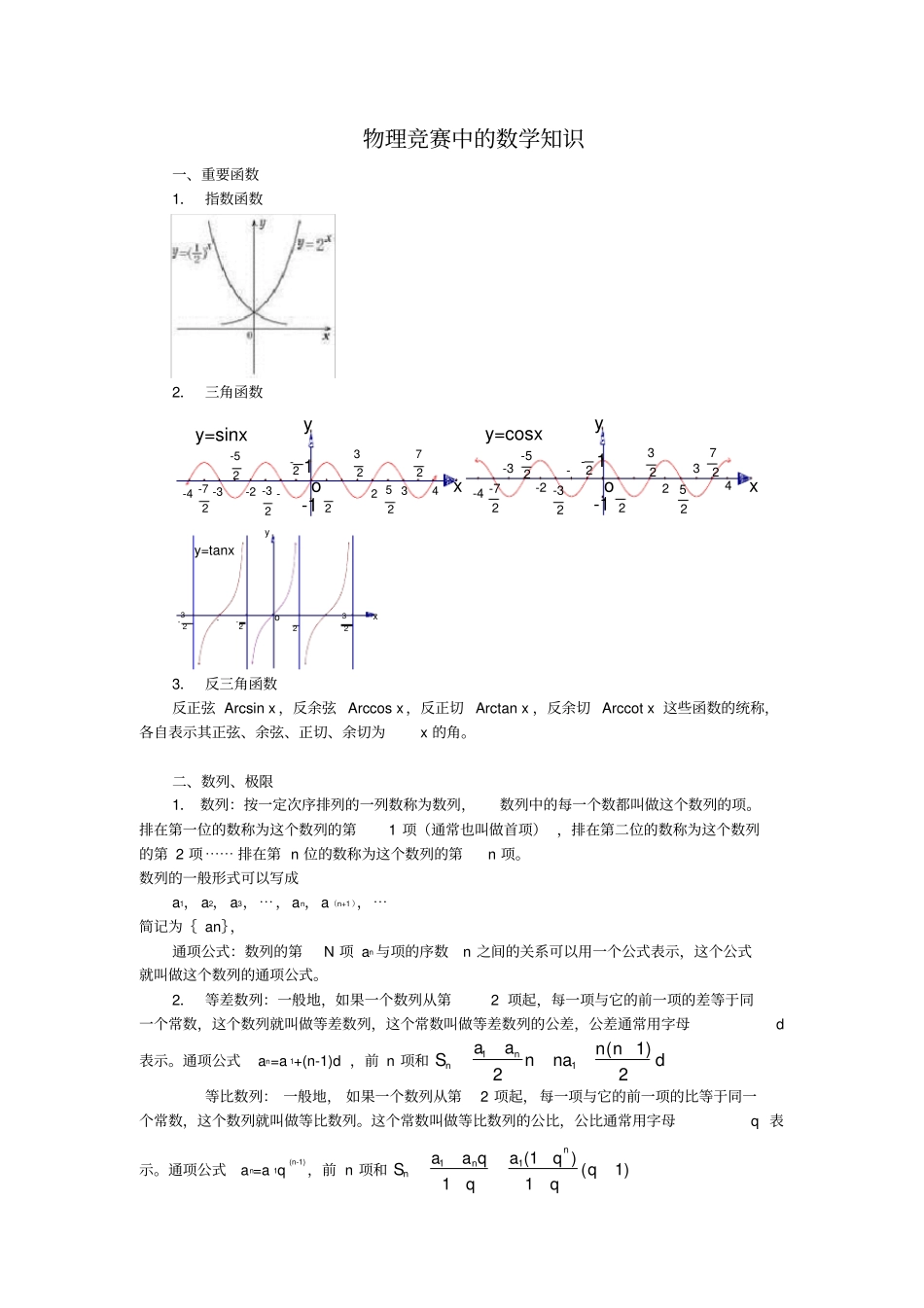
物理竞赛中的数学知识一、重要函数1. 指数函数2. 三角函数1-1y=sinx-32-52-727252322-2-4-3-2432-oyx1-1y=cosx-32-52-727252322-2-4-3-2432-oyxy=tanx322-32--2oyx3. 反三角函数反正弦 Arcsin x ,反余弦 Arccos x ,反正切 Arctan x ,反余切 Arccot x 这些函数的统称,各自表示其正弦、余弦、正切、余切为x 的角。二、数列、极限1. 数列:按一定次序排列的一列数称为数列,数列中的每一个数都叫做这个数列的项。排在第一位的数称为这个数列的第1 项(通常也叫做首项) ,排在第二位的数称为这个数列的第 2 项⋯⋯ 排在第 n 位的数称为这个数列的第n 项。数列的一般形式可以写成a1, a2, a3,⋯,an,a(n+1 ),⋯简记为{ an},通项公式:数列的第N 项 an 与项的序数n 之间的关系可以用一个公式表示,这个公式就叫做这个数列的通项公式。2. 等差数列:一般地,如果一个数列从第2 项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母d表示。通项公式an=a 1+(n-1)d ,前 n 项和11(1)22nnaan nSnnad等比数列: 一般地, 如果一个数列从第2 项起,每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列。这个常数叫做等比数列的公比,公比通常用字母q 表示。通项公式an=a 1q (n-1),前 n 项和11(1) (1)11nnnaa qaqSqqq所有项和1 (1)1naSqq3.求和符号4. 数列的极限:设数列na,当项数 n 无限增大时 ,若通项na 无限接近某个常数A ,则称数列na收敛于A,或称 A 为数列na的极限 ,记作Aannlim否则称数列na发散或nnalim不存在 . 三、函数的极限:在自变量x 的某变化过程中,对应的函数值f(x)无限接近于常数A,则称常数 A 是函数 f(x)当自变量 x 在该变化过程中的极限。设 f(x)在 x>a(a>0) 有定义 ,对任意>0, 总存在 X>0,当 x>X 时,恒有 | f(x) A|< ,则称常数A 是函数 f(x)当 x+时的极限。记为xlim f(x)=A,或 f(x) A(x+)。运算法则0limxx[f(x) g(x)]=0limxxf(x) 0limxxg(x) 0limxx[f(x) g(x)]=0limxxf(x) 0limxxg(x) )(lim)(lim)()(lim000xgxfxgxfxxxxxx,其中0limxxg(x) 0. 四、无穷小量与无穷大量1.若0)(lim0xfxx,则称)(xf是0xx时的无穷小量。(若,)(lim0xgxx则称)(xf是0xx时的无穷大量) 。或:若0limxx(x)=0 , 则称(x)当 x x0时为无穷小。在自变量某变化过程...