天津大学版工程力学习题答案(部分)

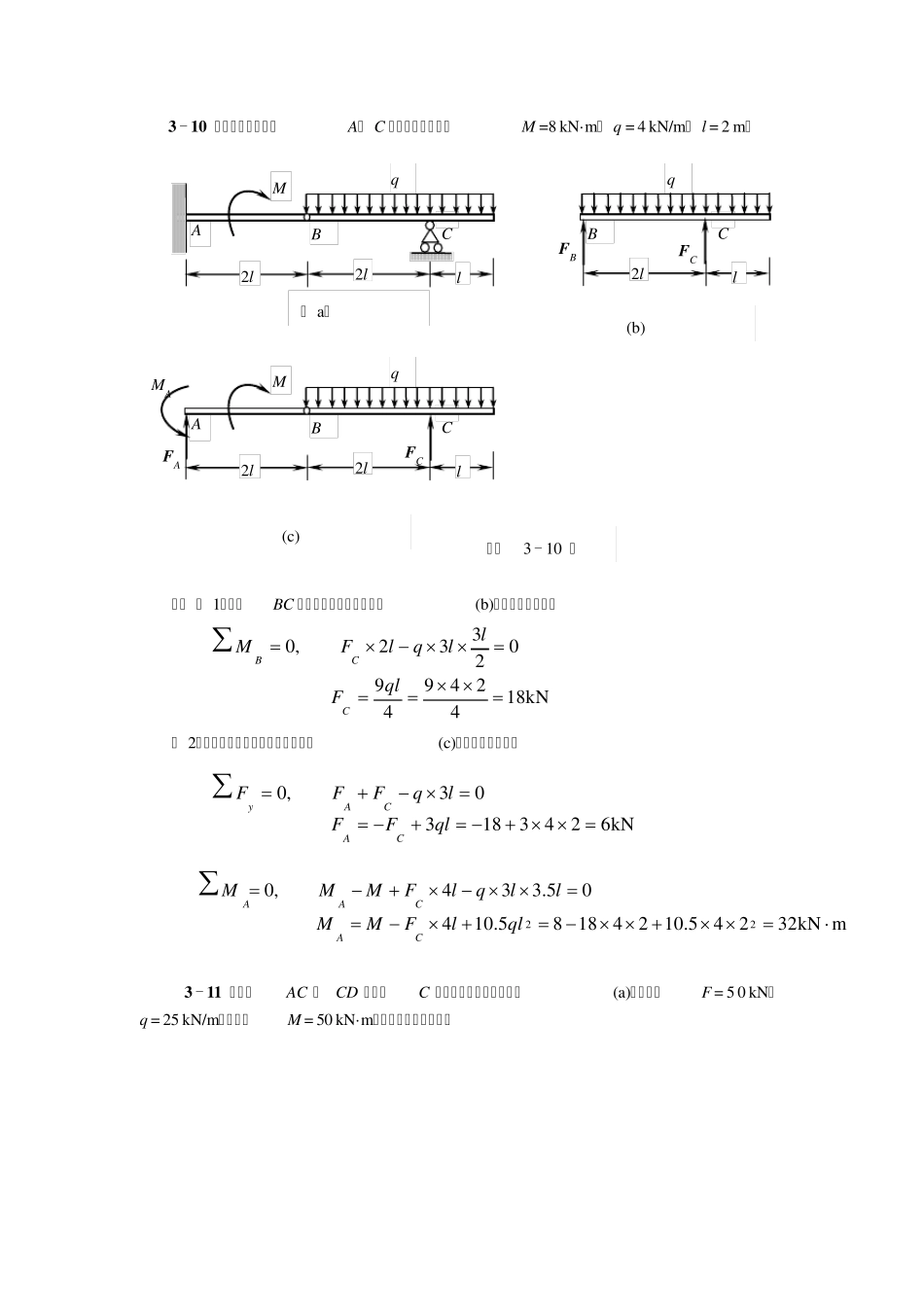
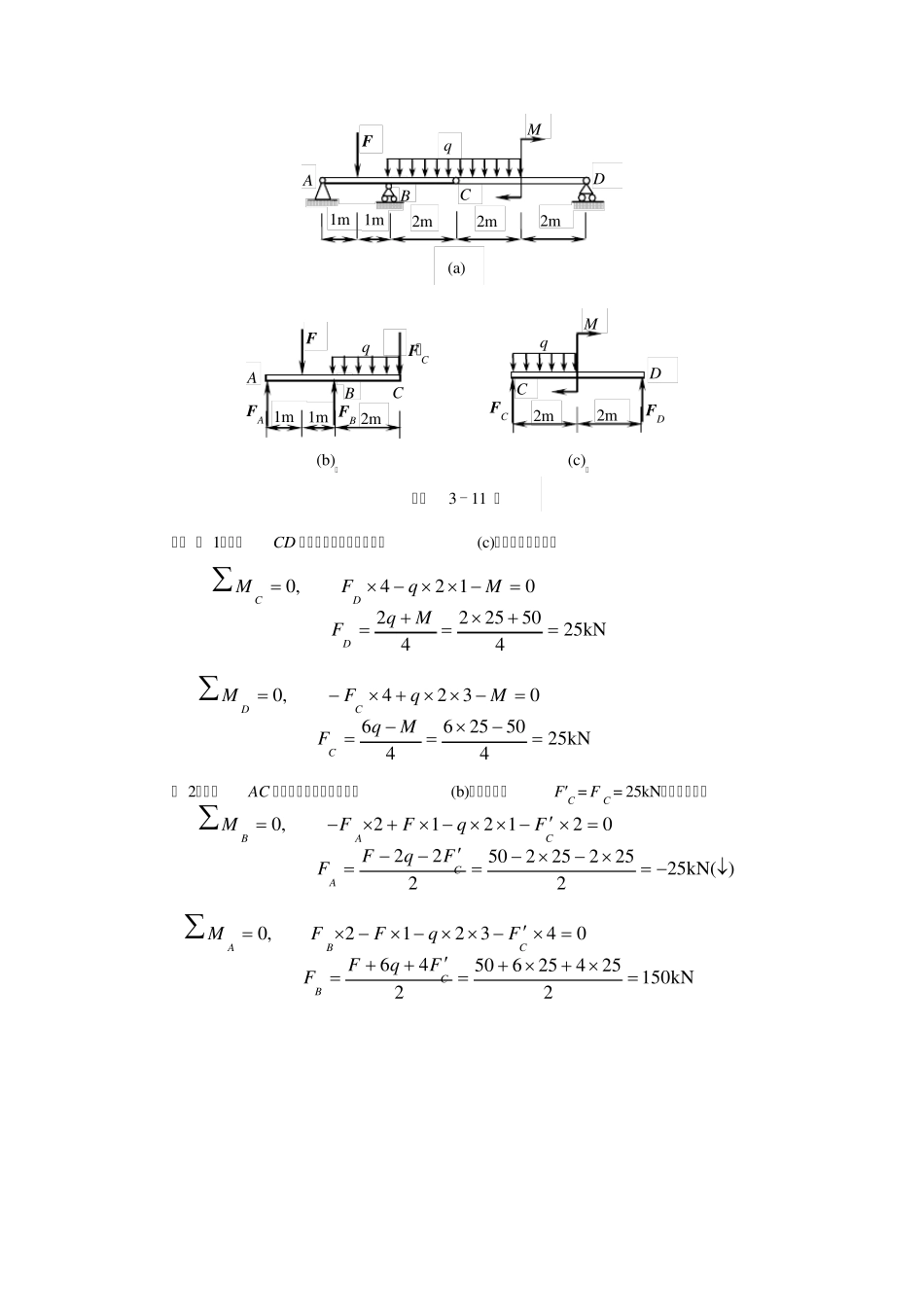
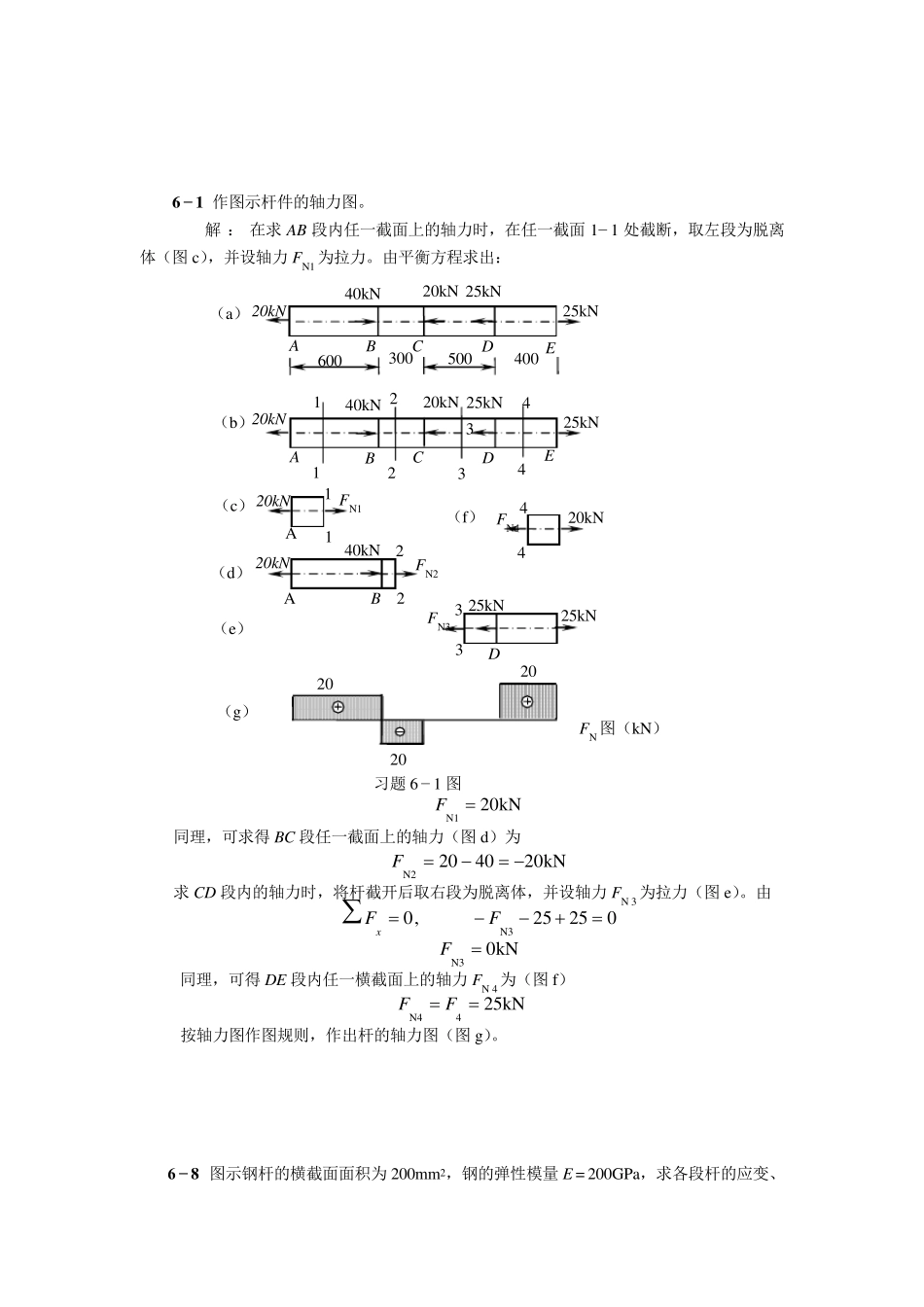
3 - 1 0 求图示多跨梁支座A、 C 处的约束力。已知M =8 kN·m， q = 4 kN/m， l = 2 m。 解： （ 1）取梁BC 为研究对象。其受力如图(b)所示。列平衡方程 （ 2）取整体为研究对象。其受力如图(c)所示。列平衡方程 3 - 1 1 组合梁 AC 及CD 用铰链C 连接而成，受力情况如图(a)所示。设F = 5 0 kN，q = 25 kN/m，力偶矩M = 50 kN·m。求各支座的约束力。 B q 2l l C FB FC (b) M (c) B q A 2l l 2l C FC MA FA M （ a） B q A 2l l 2l C 习题3 - 10 图 kN1842494902332,0qlFllqlFMCCBkN624318303,0qlFFlqFFFCACAymkN32245.10241885.10405.334,022qllFMMllqlFMMMCACAA 解： （ 1）取梁CD 为研究对象。其受力如图(c)所示。列平衡方程 （ 2）取梁AC 为研究对象。其受力如图(b)所示，其中F′C = F C = 25kN。列平衡方程 习题3 - 11 图 2m 2m C D M q F C F D 2m 1m 2m 2m 1mC BD A M F (a) q (b)一 (c)一 F ´C 1m 2m 1mBA F F A F B q C kN25450252420124,0MqFMqFMDDCkN25450256460324,0MqFMqFMCCD)kN(25225225250222021212,0CACABFqFFFqFFMkN150225425650246043212,0CBCBAFqFFFqFFM 6 − 1 作图示杆件的轴力图。 解：在求AB 段内任一截面上的轴力时，在任一截面1− 1 处截断，取左段为脱离体（图c），并设轴力FN1为拉力。由平衡方程求出： kN201N F 同理，可求得BC 段任一截面上的轴力（图d）为 kN204020N2F 求CD 段内的轴力时，将杆截开后取右段为脱离体，并设轴力FN 3为拉力（图e）。由 kN002525,0N3N3FFFx 同理，可得DE 段内任一横截面上的轴力FN 4为（图f） kN254N4 FF 按轴力图作图规则，作出杆的轴力图（图g）。 6 − 8 图示钢杆的横截面面积为200m m 2，钢的弹性模量E = 200GPa，求各段杆的应变、600 300 500 400 A B C D E 40kN 20kN 25kN 25kN （a） A B C D E 40kN 20kN 25kN 25kN 20kN 1 1 FN2 A B 40kN 2 2 2 2 3 3 4 4 FN3 25kN ...