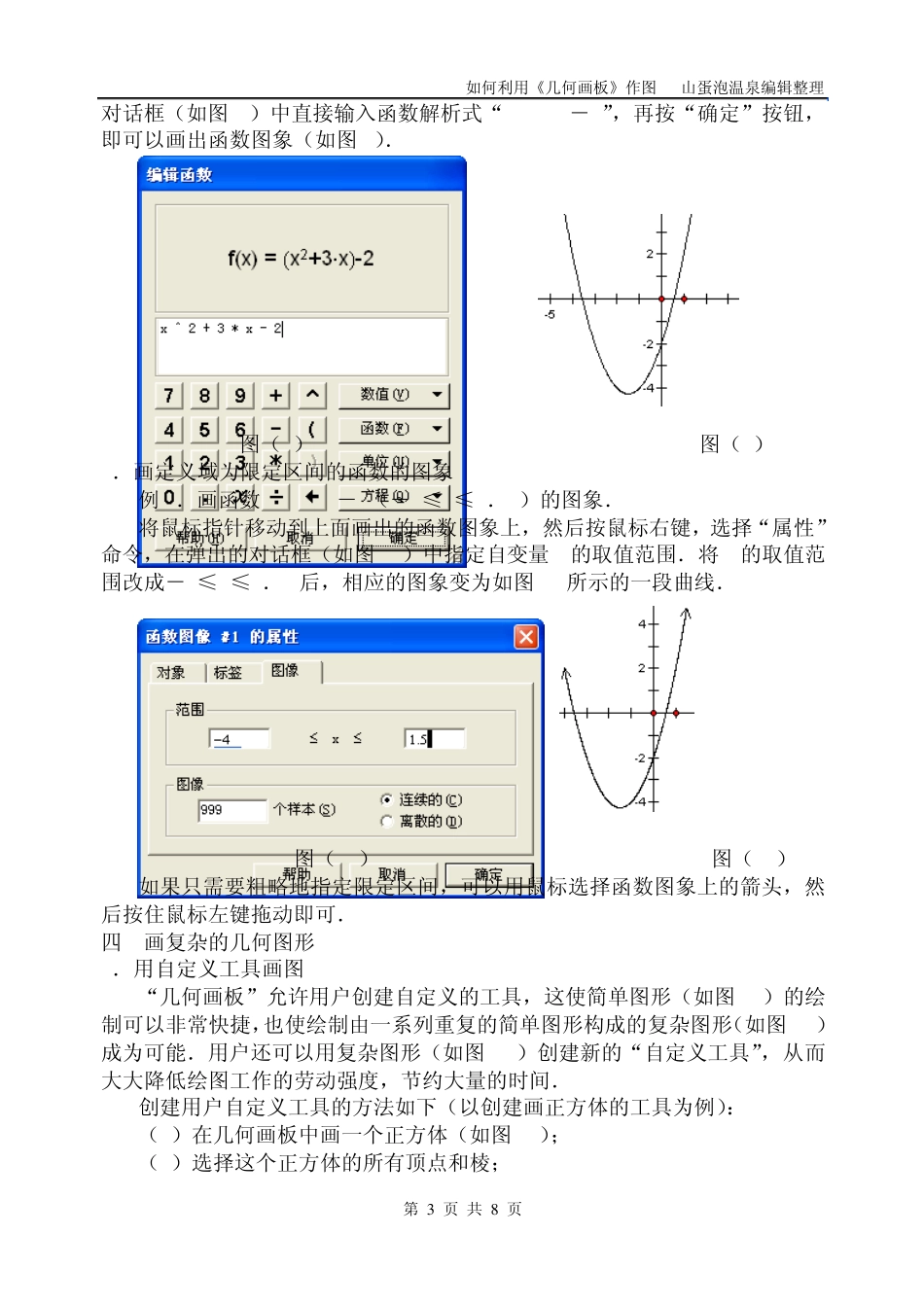
如何利用《几何画板》作图 山蛋泡温泉编辑整理 第 1 页 共 8 页 如何利用《几何画板》作图 在中学数学教学工作中，我们经常会遇到需要画图的情况．笔者以自己在工作中所遇到的实际问题为例，说明如何应用几何画板画出符合要求的图形，并简要说明这些画图方法正确及可行的理论依据． 一 画简单的几何图形 1．按已知条件画几何图形 例 1．已知：梯形 ABCD中．AD∥BC．AB=AD+BC．E是 CD的中点．求证：AE、BE分别平分∠BAD、∠ABC． 如图 1，我们可以从已知条件出发，按照以下操作步骤，画出符合例 1的题意的图形． （1）画出腰 AB和两底所在的射线； （2）在线段 AB上任取一点 F，分别以点 A、B为圆心，以 AF、BF长为半径作圆，与两底所在的射线交于点 D、C．显然，AD+BC=AB． （3）取线段 CD的中点 E，连结 AE、BE； （4）将作图过程中的辅助图形隐藏，即可得到符合题目要求的图形（如图2）． FEDCBA EDCBA GEDCBA EDCBA 图（1） 图（2） 图（3） 图（4） 2．从结论出发画几何图形 若要证明的命题的逆命题也成立，则可以从结论出发画出几何图形． 仍以例 1为例．例 1的逆命题是：在梯形 ABCD中，AD∥BC，∠DAB和∠CBA的平分线交于点 E，点 E恰好在腰 CD上．则：AB=AD+BC，E是 CD的中点． 显然，∠AEB=90°．如图 3，设线段 AB的中点是点 G，连结 EG，则AG=EG，即：∠AEG=∠EAG=∠EAD．所以 AD∥EG，因此，CE=DE，AD+BC=2EG=AB． 由于例 1的逆命题是真命题，所以我们可以从例 1的结论出发画出符合题意的几何图形．画图步骤如下： （1）如图 4，画出腰 AB和两底所在的射线； （2）作∠A和∠B的角平分线，交于点 E； （3）在一底所在的射线上任取一点 C，
