相交线与平行线基础证明训练

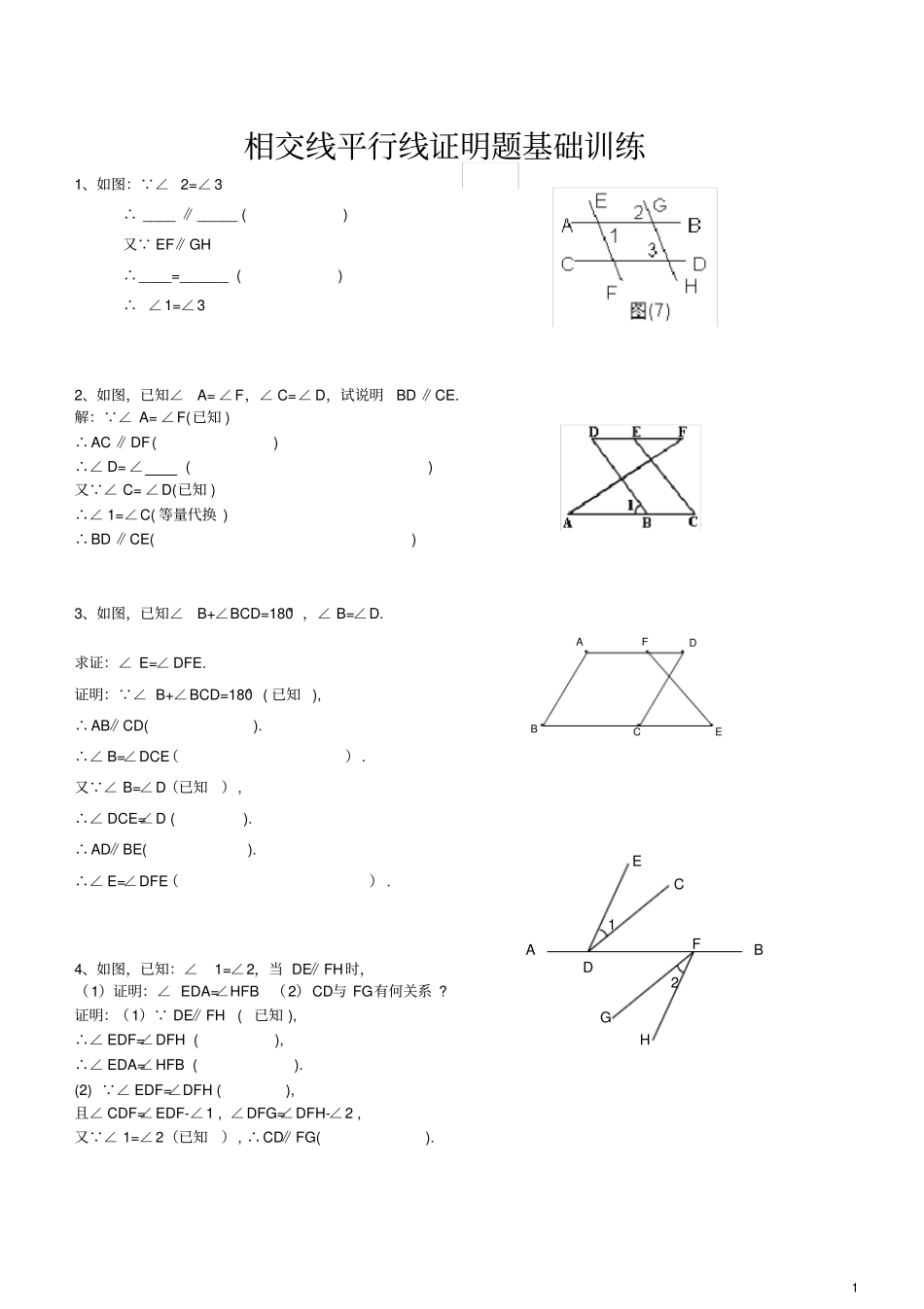
1 相交线平行线证明题基础训练1、如图： ∠ 2=∠ 3 ∴ ____ ∥_____ ( ) 又 EF∥GH ∴____=______ ( ) ∴ ∠1=∠3 2、如图，已知∠A= ∠F，∠ C=∠ D，试说明BD ∥CE. 解： ∠ A= ∠F(已知 ) ∴AC ∥DF( )∴∠ D= ∠( ) 又 ∠ C= ∠D(已知 ) ∴∠ 1=∠C( 等量代换 ) ∴BD ∥CE( ) 3、如图，已知∠B+∠BCD=180° ，∠ B=∠D. 求证：∠ E=∠ DFE. 证明： ∠ B+∠BCD=180° ( 已知 ), ∴AB∥CD( ). ∴∠ B=∠DCE（）. 又 ∠ B=∠D（已知）, ∴∠ DCE=∠D ( ). ∴AD∥BE( ). ∴∠ E=∠DFE（） . 4、如图，已知：∠1=∠2，当 DE∥FH时，（1）证明：∠ EDA=∠HFB （2）CD与 FG有何关系 ? 证明：（1） DE∥FH (已知 ), ∴∠ EDF=∠DFH ( ),∴∠ EDA=∠HFB ( ).(2) ∠ EDF=∠DFH ( ), 且∠ CDF=∠EDF-∠1 , ∠DFG=∠DFH-∠2 , 又 ∠ 1=∠2（已知）, ∴CD∥FG( ). DABECFA B E C G H F 1 2 D 2 GHKFEDCBA5、如右图 ,已知 AD⊥BC,EF⊥BC,∠1=∠2. 求证 :DG∥BA. 证明： AD ⊥BC,EF ⊥BC ( ) ∴∠ EFB= ∠ADB=90 °( ) ∴EF∥AD( ) ∴∠ 1=∠BAD( ) 又 ∠ 1=∠2 ( ) ∴（等量代换）∴DG ∥BA.( ) 6、如图：已知：AD ⊥BC 于 D，EF ⊥BC 于 F，∠ 1=∠3，求证：AD 平分∠ BAC 。证明： AD⊥ BC EG⊥BC于 F（已知）∴AD∥ EF（）∴∠ 1＝∠ E（）∠2＝∠ 3（）又 ∠ 3＝∠ E（已知）∴∠ 1＝∠ 2（）∴AD平分∠ BAC（）7、如图所示 , 已知直线 EF和 AB,CD分别相交于K,H, 且 EG⊥AB,∠ CHF=600, ∠E=30° , 试说明 AB∥CD. 证明： EG ⊥AB （已知）∴∠ EGK=90 ° ( ), ∴ 在Δ EGK中∠ E+∠EKG=90 ° （），又 ∠ E=30 ° （）∴∠ EKG=60 0 又 ∠ CHF=60 0 ∴∠ EKG= ∠CHF ∴AB ∥CD. （）。8、已知：如图 ,AB∥CD，AD∥BC. 求证：∠ A＝∠ C . 证明： AB∥CD，（_______________）∴∠ B+∠C=180° . （____________________________ ） AD∥ BC，（已知）∴∠ A+∠B=180° . （________________________ ）∴∠ A＝∠ C . (_____________________________) A B C D 3 9. 已知，如图， AD∥BC，∠ BAD=∠BCD，请说明 AB∥CD的理由 . 理由： AD∥BC(已知 ) ∴∠ 1=( )( ) 又...