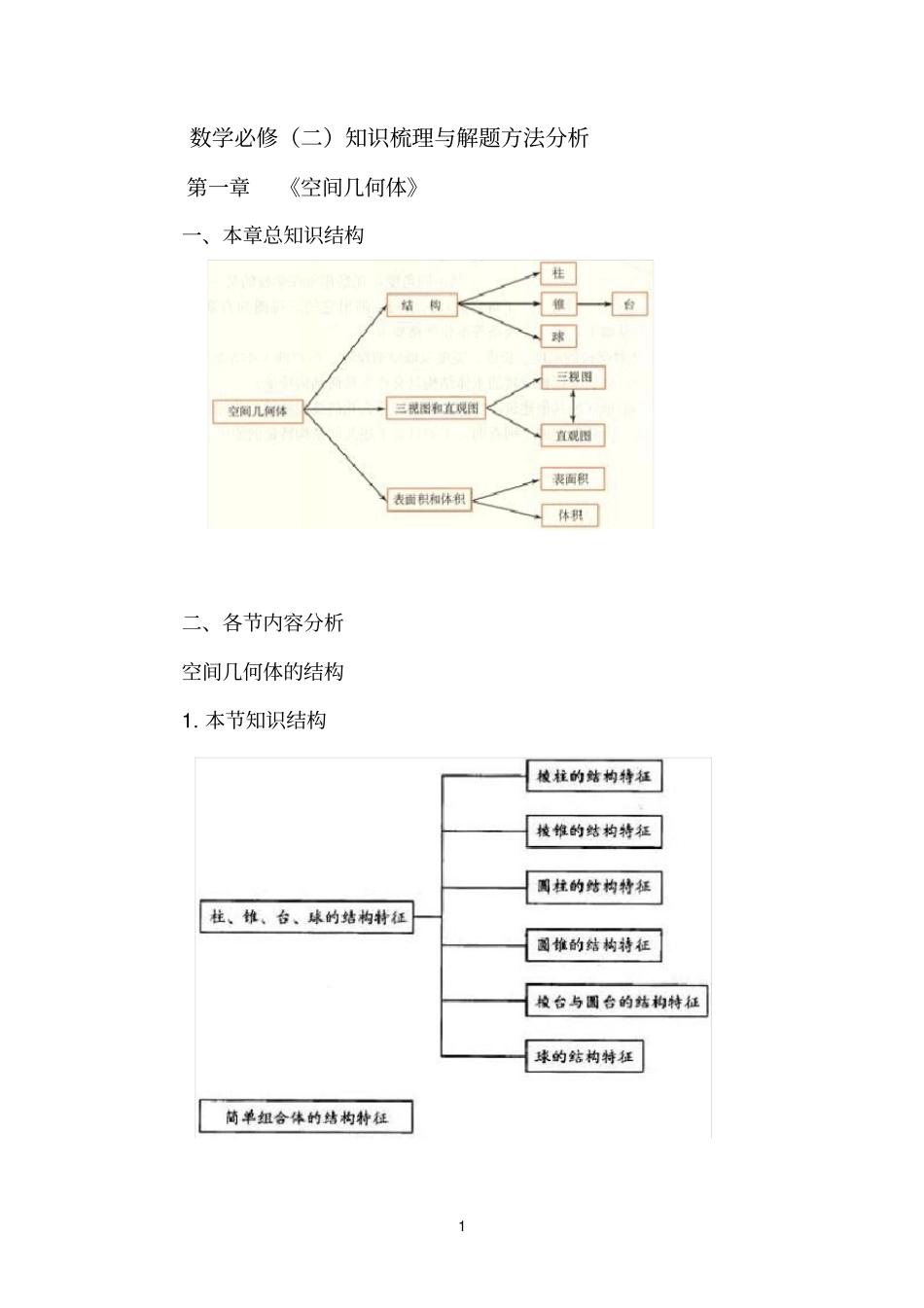
1 数学必修(二)知识梳理与解题方法分析第一章《空间几何体》一、本章总知识结构二、各节内容分析空间几何体的结构1. 本节知识结构2 空间几何体三视图和直观图1、本节知识结构空间几何体的表面积与体积1、本节知识结构。三、高考考点解析本部分内容在高考中主要考查以下两个方面的内容:1. 多面体的体积(表面积)问题;2. 点到平面的距离(多面体的一个顶点到多面体一个面的距离)问题—“等体积代换法” 。(一)多面体的体积(表面积)问题1. 在四棱锥P-ABCD中,底面是边长为2 的菱形,∠ DAB=60 ,对角线AC与 BD相交于点 O,PO⊥平面 ABCD,PB与平面 ABCD所成的角为60 .(1)求四棱锥P-ABCD的体积;【解】( 1)在四棱锥P-ABCD中, 由 PO⊥平面 ABCD,得∠PBO是 PB与平面 ABCD所成的角 , ∠PBO=60° .在 Rt△AOB中 BO=ABsin30° =1, 由PO⊥BO,于是, PO=BOtan60° =3 ,3 而底面菱形的面积为23 .∴四棱锥 P-ABCD的体积 V=31 ×23 ×3 =2.2.如图 , 长方体 ABCD-1111DCBA中,E、P 分别是 BC、11A D 的中点 ,M、N分别是 AE、1CD的中点,1AD=AA,a AB=2 ,a(Ⅲ)求三棱锥P-DEN的体积。【解】(Ⅲ)111124NEPECD PSSBC CD矩形22215444aaaa作1DQCD ,交1CD 于 Q ,由11A D面11CDD C 得11ACDQ∴ DQ面11BCD A∴在1Rt CDD 中,112255CD DDa aDQaCDa∴13PDENDENPNEPVVSDQ21523 45aa316a 。(二)点到平面的距离问题—“等体积代换法”。1 如图,四面体ABCD中, O、E 分别是 BD、BC的中点,2,2.CACBCDBDABAD(III)求点 E 到平面 ACD的距离。【解】(III ) 设点 E到平面 ACD的距离为.hEACDA CDEVV,∴ 11.33ACDCDEh SAO S在ACD中,2,2,CACDAD2212722().222ACDS而21331,2,242CDEAOSCADBOE4 31.212.772CDEACDAO ShS点 E 到平面 ACD的距离为21 .72.如图,已知正三棱柱111ABCA B C 的侧棱长和底面边长为 1,M 是底面 BC 边上的中点, N 是侧棱1CC 上的点,且12CNC N=。(Ⅱ)求点1B 到平面 AMN 的距离。【解】(Ⅱ)过1B 在面11BCC B 内作直线1B HMN , H 为垂足。又 AM平面11BCC B ,所以 AM1B H 。于是1B H平面AMN,故1B H 即为1B 到平面 AMN的距离。在11RB HM 中,1B H=1B M151sin1125B MH。故点1B 到平面 AMN的距离为 1。3 如图, 已知三棱锥 OABC 的侧棱 OAOBOC、、两两垂直,且 OA=1,OB=OC=2, E 是...