应用数理统计公式总结

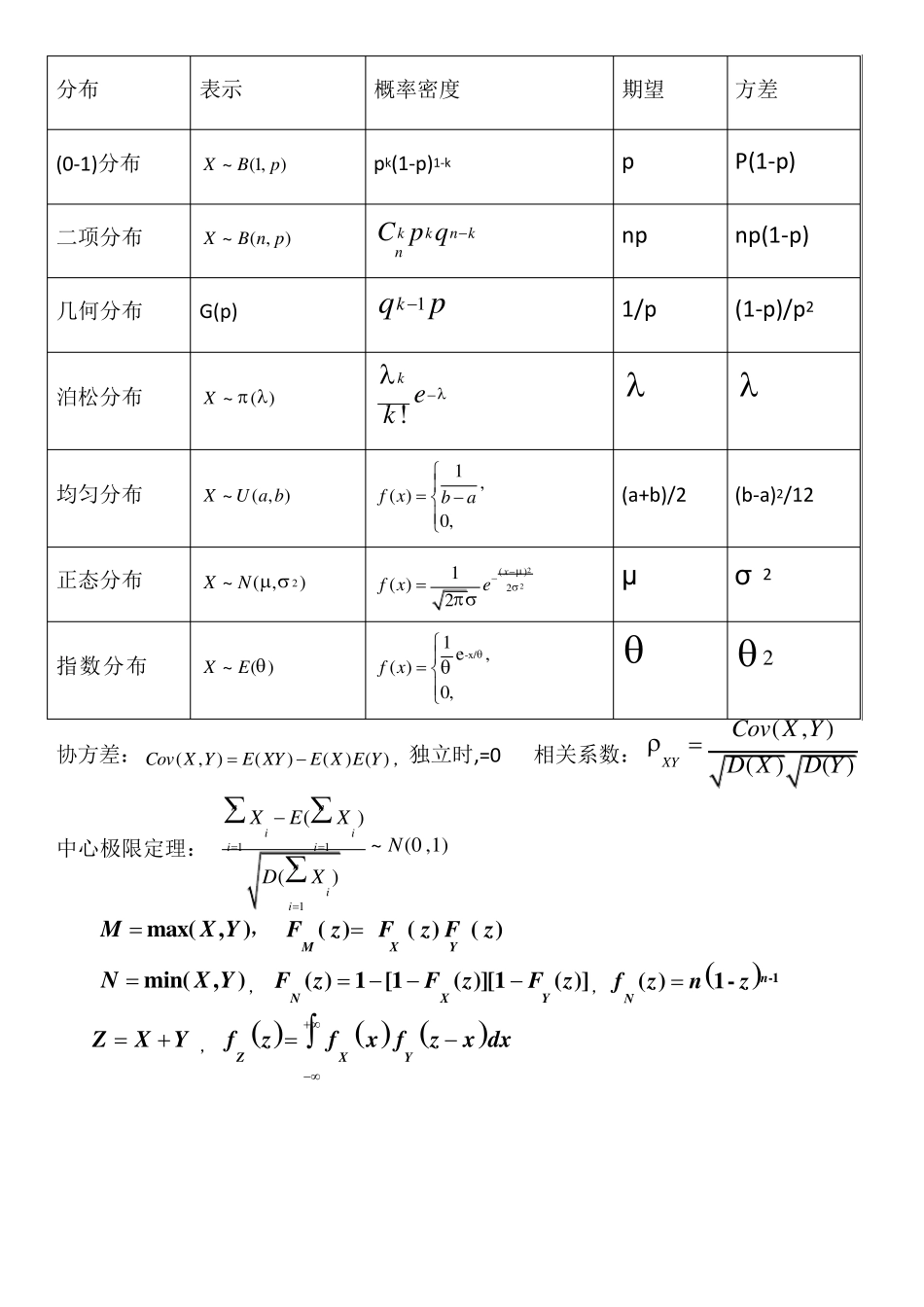
分布 表示 概率密度 期望 方差 (0-1)分布 ~(1,)XBp pk(1-p)1-k p P(1-p) 二项分布 ~( , )XB n p kkn knC p q  np np(1-p) 几何分布 G(p) 1kqp 1/p (1-p)/p2 泊松分布 )(~X !k ek   均匀分布 ~( , )XU a b 1,( )0,f xba (a+b)/2 (b-a)2/12 正态分布 2~( ,)XN   22()21( )2xf xe μ σ 2 指数分布 ~( )XE  -x/1 e,( )0,f x   2 协方差：(, )()() ( )Cov X YE XYE X E Y，独立时,=0 相关系数：(, )()( )XYCov X YD XD Y 中心极限定理： 111()~(0 ,1)()nniiiiniiXEXNDX max(, )MX Y， ( )( )( )MXYFzFz Fz min(,)NX Y， ( )1[1( )][1( )]NXYFzFzFz， -1( )1-nNfznz ZXY，  ZXYfzfx fzx dx 222211111,1nnniiiiiiXXSXXXnXnn ()()E XE X 2()()D XD Xnn 22()E S 422()-1D Sn 241()2I  21( )I  2 分布：设12,,,nXXX 相互独立, 都服从正态分布N (0,1)，则称随机变量：222212nXXX 所服从的分布为自由度为n 的2 分布记为22~( )n t分布：设X～N(0,1) , 2( )Yn～，且X 与 Y 相互独立，则称变量 XtY n 服从自由度为n 的t分布.记为 t～t (n). F 分布：设2212~( ),~(),XnYnX 与 Y 相互独立，则称统计量 12X nFY n服从自由度为12,n n的F 分布，记作12~( ,)FF n n 112211( ,)(,)Fn nF n n 抽样分布：2(1)~( ,)XNn ~( 0 , 1 )XNn 222(1 )( 2 )~(1 )nSn ( 3 )~(1 )Xt nSn 2211122222(4)~(1,1)SF nnS2212(5)~(,)XYNnm1222()()(6)~(0,1)XYNnm 2221222(1)(1)(7)~(2)nSmSnm 122212()()(8)~ (2)(1)(1)112XYt nmnSmSnmnm 距估计：222212()，EXEXDXEX 21211,niiAXAXn  2222222111111ˆ()nniiiinAAXXXXSnnn 极大似然估计：1、写出似然函数：1( )( ; )niiLf x或 1( )( ; )niiLp x 2、取对数ln( )L  3、求导...