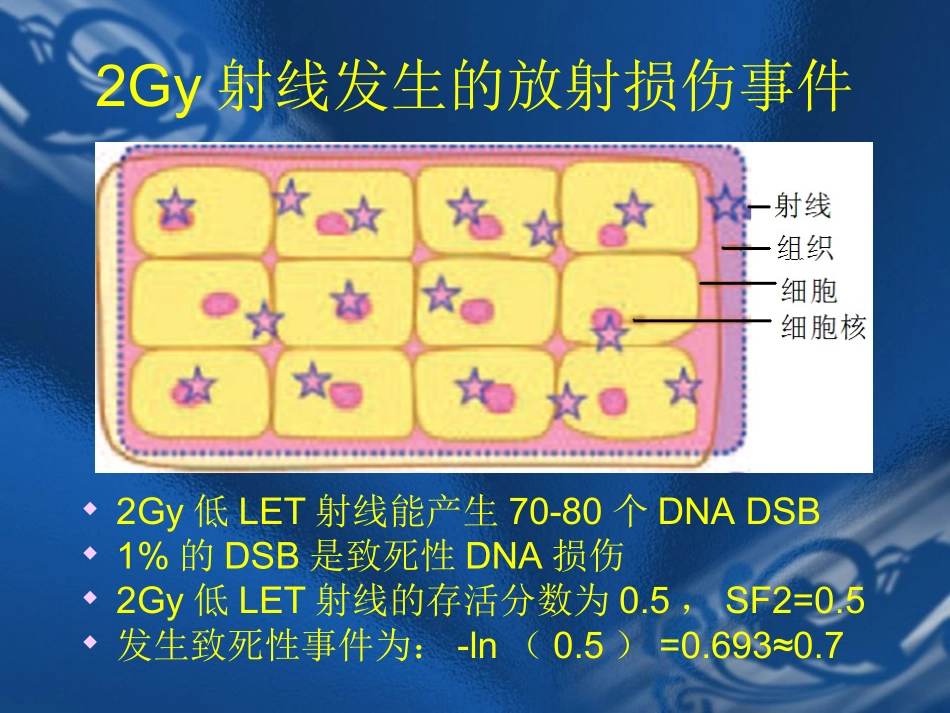
SBRT的临床放射生物学模型放射生物学的四维问题物理生物空间位置剂量分布时间运动分次2Gy射线发生的放射损伤事件2Gy低LET射线能产生70-80个DNADSB1%的DSB是致死性DNA损伤2Gy低LET射线的存活分数为0.5,SF2=0.5发生致死性事件为:-ln(0.5)=0.693≈0.7放射实验获得的细胞生存曲线早期提出的放射生物学模型Power-lawmodel(Strandqvist,1944)NSD(Ellis,1967)CRE(Kirk,1971)TDF(Orton&Ellis,1973)Neuret(Sheline,1980)Opticret(Goldsmith,etal.,1992)问题所在临床生物化学物理机械学说现象学说没有考虑到射线的性质、特征没有意识到细胞的结构、功能没有区分不同组织的放射反应机械学说物理:光电子、康普顿、电子对电离或激发化学:自由基生物:染色体/DNA分子/基因结局:细胞凋亡或分裂失去再增殖能力临床:细胞生存曲线,在体、离体的定量分析靶学说生物物理学说(F.Dessauer,1922)放射效应是电子冲击蛋白质分子而导致显微能量吸收和温度升高所为,启迪了击中理论(Hittheory)靶细胞假说(Target-CellHypothesis)生物组织的放射效应乃含有放射靶标的细胞之存活几率改变所引起存活=细胞繁殖的永续不竭靶标=细胞染色体或DNA放射线击中靶细胞概率-水桶理论在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变,则这一系列试验总称为n重伯努利实验,当试验次数为1时,二项分布就是伯努利分布射线击中细胞的二项分布实验中细胞被射线击中后死亡概率P,则生存概率为=1-P故:对一个射线粒子进行实验的结果为:击中(死亡概率为P)或未击中(生存概率为1-P)对二个射线粒子(甲乙)进行实验的结果为:甲乙均死(概率为P2)、甲死乙生[概率为P(1-P)]、乙死甲生[概率为(1-P)P]或甲乙均生[概率为(1-P)2],概率相加得P2+P(1-P)+(1-P)P+(1-P)2=[P+(1-P)]2依此类推,对n个射线粒子进行实验,所有可能结果的概率相加得Pn+cn1P(1-P)n-1+...+cnxPx(1-P)n-x+...+(1-P)x=[P+(1-P)]n二项分布是说明结果只有两种情况的n次实验中发生某种结果为x次的概率分布。其概率密度为:其中n为样本含量,即事件发生总数,x为某事件出现次数,x=0,1,...n。泊松分布Poisson分布是二项分布n很大而P很小时的特殊形式,是两分类资料在n次实验中发生x次某种结果的概率分布。Poisson分布的应用条件:医学领域中有很多资料都符合Poisson分布,但应用中需满足以下条件:(1)两类结果要相互对立;(2)n次试验相互独立;(3)n应很大,P应很小。二项分布泊松分布泊松分布常用于描述单位时间、单位平面或单位空间中罕见质点总数的随机分布规律,罕见质点的发生数为X,其概率密度函数为:P(x)=x=0,1,2...n,其中e为自然对数的底,λ为总体均数发生率,ι为事件发生的阳性数。Poisson分布的概率细胞未被击中的概率,即X=ι=0,递推公式很容易求得:P(0)=e-λ单击模型(SingleHit,SH)λ=1,SF≈37%细胞生存:P(0)=e-λλ=2,SF≈14%λ=3,SF≈5%假设:雨滴数为N,有K个水桶,雨滴滴入水桶是随机的,而且所有雨滴都没有滴到水桶外那:每个桶平均雨滴数为N/K显然:λ为每个水桶平均雨滴量,也就是每个细胞平均受射线粒子击中次数,显然和放射剂量(雨滴数)有关单击模型的λ定义假设:总的放射粒子数(总雨滴数)为剂量D每个细胞平均受到一次击中的粒子数(每个水桶滴入一滴雨滴量)为剂量1D0那:每一个细胞平均被粒子击中的数量λ(每一个水桶平均滴入的雨滴量)为D/1D0因此:SF=P(0)=e-λ=e-D/1D0单击模型的细胞生存曲线SF=e-D/1D0lnSF=lne-D/1D0=-D/1D0单击模型的意义定义:细胞内一个敏感靶区被电离粒子击中一次,引起细胞死亡,称为单靶单击灭活(singlehitsingle-targetinactivation)单击模式可表述为细胞靶区受到一次性的致命打击,而根本无从加以修复。DNA分子的双链断裂,细胞失去增殖能力此模型适用于:1.能够描述某些非常敏感的人体正常组织和肿瘤组织的辐射生物效应2.能够描述高LET辐射生物效应和在低剂量率情况下的辐射生物...