数值分析实验题答案

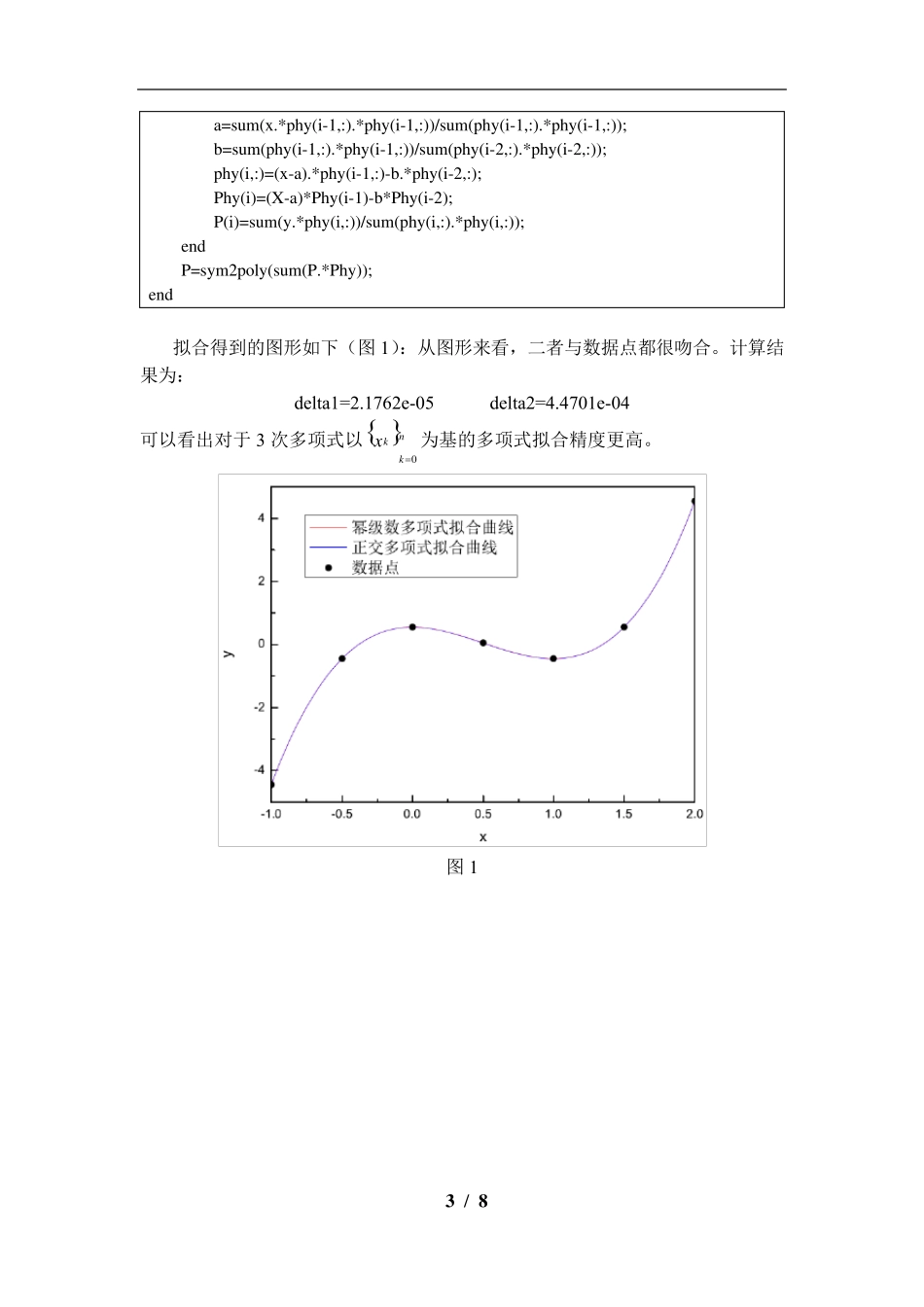
数值分析实验报告 姓名： 院系：能源学院热能工程 学号： 2014 年 4 月 2 / 8 习题一 实验 3.2 编制正交化多项式最小二乘拟合程序，并用于求解3 次多项式最小二乘拟合问题，作拟合曲线的图形，计算平方误差，并与以函数 0nkkx为基的多项式最小二乘拟合的结果作比较 表1 ix -1.0 -0.5 0.0 0.5 1.0 1.5 2.0 iy -4.447 -0.452 0.551 0.048 0.447 0.549 4.552 首先使用以函数 0nkkx为基的多项式最小二乘拟合，代码如下： x=linspace(-1,2,7); y=[-4.447,-0.452,0.551,0.048,-0.447,0.549,4.552]; for i=1:4 for j=1:4 A(i,j)=sum(x.^(3+i-j)); end B(i)=sum(y.*x.^(i-1)); end al=A\B'; deltal=sum((polyval(al,x)-y).^2); 然后使用正交化多项式方法作最小二乘拟合并画图，代码如下： [P,phy]=orthpoly(x,y,3); delta2=sum((polyval(P,x)-y).^2); plot(x1,polyval(a1,x1),’r-’,x1,polyval(P,x1),’b-’,x,y,’k.’); %orthpoly fuction function[P,phy]=orthpoly(x,y,k) symsX; phy=zeros(k+1,length(x)); phy(1,:)=1; P(1)=sum(y)/length(x); a=sum(x.*phy(1,:).*phy(1,:))/sum(phy(1,:).*phy(1,:)); phy(2,:)=x-a; Phy(1)=sym(1); Phy(2)=X-a; P(2)=sum(y.*phy(2,:))/sum(phy(2,:).*phy(2,:)); for i=3:k+1 3 / 8 a=sum(x.*phy(i-1,:).*phy(i-1,:))/sum(phy(i-1,:).*phy(i-1,:)); b=sum(phy(i-1,:).*phy(i-1,:))/sum(phy(i-2,:).*phy(i-2,:)); phy(i,:)=(x-a).*phy(i-1,:)-b.*phy(i-2,:); Phy(i)=(X-a)*Phy(i-1)-b*Phy(i-2); P(i)=sum(y.*phy(i,:))/sum(phy(i,:).*phy(i,:)); end P=sym2poly(sum(P.*Phy)); end 拟合得到的图形如下（图1）：从图形来看，二者与数据点都很吻合。计算结果为： delta1=2.1762e-05 delta2=4.4701e-04 可以看出对于 3 次多项式以 0nkkx为基的多项式拟合精度更高。 图1 4 / 8 习题二 实验 4.2 分别用复化Simpson 公式与变步长Simpson 公式计算，要求绝对误差限为71=102，输出每种方法所需的节点数和积分近似值并分析比较结果。 （1）6220()10xxx dx （2）10x xdx （3）6220()10xxx dx 对于复化Simpson 公式，使用事前误差估计法得到所需计算节点数，有以下误差估计公式： 4(4)()( )( )( ),( , )1802nbahRffa b   对（1）式有： (4)22max( )36144x...