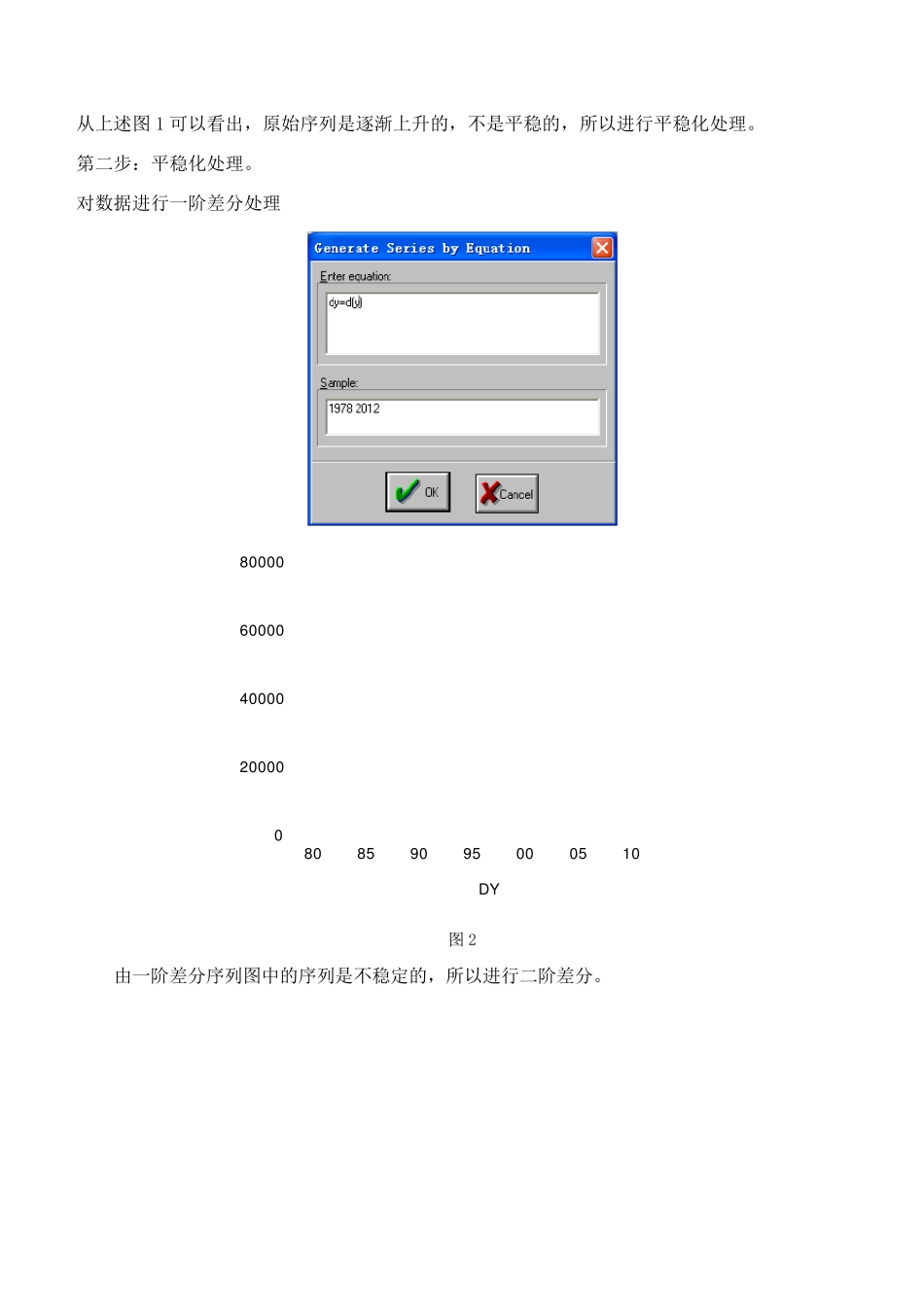
课 程 名 称:__ 时间序列分析 __ 实 验 项 目:__ ARMA 模型 ______ 实 验 类 型:__ 验证型_______ ___ 学 生 学 号:__ 2012962016 ______ 学 生 姓 名:__ 张艳杰 _________ 学 生 班 级:_ 统计学________ ___ 课 程 教 师:__ 范英兵______ _____ 实 验 日 期:_______ 2014 年 10 月 13 日_____ 1.实验目的: 通过实验掌握ARMA 模型的建立步骤;掌握如何分析ARMA 模型;掌握ARMA 模型的滞后阶数的确定;理解ARMA 模型建立的前提。 2.实验内容 (1)序列的平稳性检验。 (2)平稳化处理。 (3)根据平稳序列的自相关函数和偏自相关函数确定模型类型。 (4)模型阶数确定。 (5)建立模型。 (6)模型预测。 3.实验步骤 第一步:选取 1970 年到 2004 年的GNP,进行平稳性检验。 1970 3645.2 1977 9016.0 1984 26923.5 1991 89677.1 1998 216314.4 1971 4062.6 1978 10275.2 1985 35333.9 1992 99214.6 1999 265810.3 1972 4545.6 1979 12058.6 1986 48197.9 1993 109655.2 2000 314045.4 1973 4891.6 1980 15042.8 1987 60793.7 1994 120332.7 2001 340902.8 1974 5323.4 1981 16992.3 1988 71176.6 1995 135822.8 2002 401512.8 1975 5962.7 1982 18667.8 1989 78973.0 1996 159878.3 2003 473104.0 1976 7208.1 1983 21781.5 1990 84402.3 1997 184937.4 2004 518942.1 将数据导入 Eviews 中,做序列图。 010000020000030000040000050000060000080859095000510Y 图 1 从上述图1 可以看出,原始序列是逐渐上升的,不是平稳的,所以进行平稳化处理。 第二步:平稳化处理。 对数据进行一阶差分处理 02000040000600008000080859095000510DY 图2 由一阶差分序列图中的序列是不稳定的,所以进行二阶差分。 -40000-200000200004000080859095000510DDY 图3 由一阶差分序列图中的数据在0 附近波动可以看出序列是稳定的。 第三步:根据平稳序列的自相关函数和偏自相关函数确定模型类型。 自相关与偏自相关都是拖尾的,MA 做1 或2 阶,AR 做1 阶。所以建立 ARMA 模型。 第四步:模型阶数的确定。 在命令窗口输入命令:ls ddy ar(1) ma(1) c Variable Coefficient Std. Error t-Statistic Prob. C 1760.451 800.2220 2.199954 0.0359 AR(1) 0.098614 0....