抗扭承载力分解VIP免费

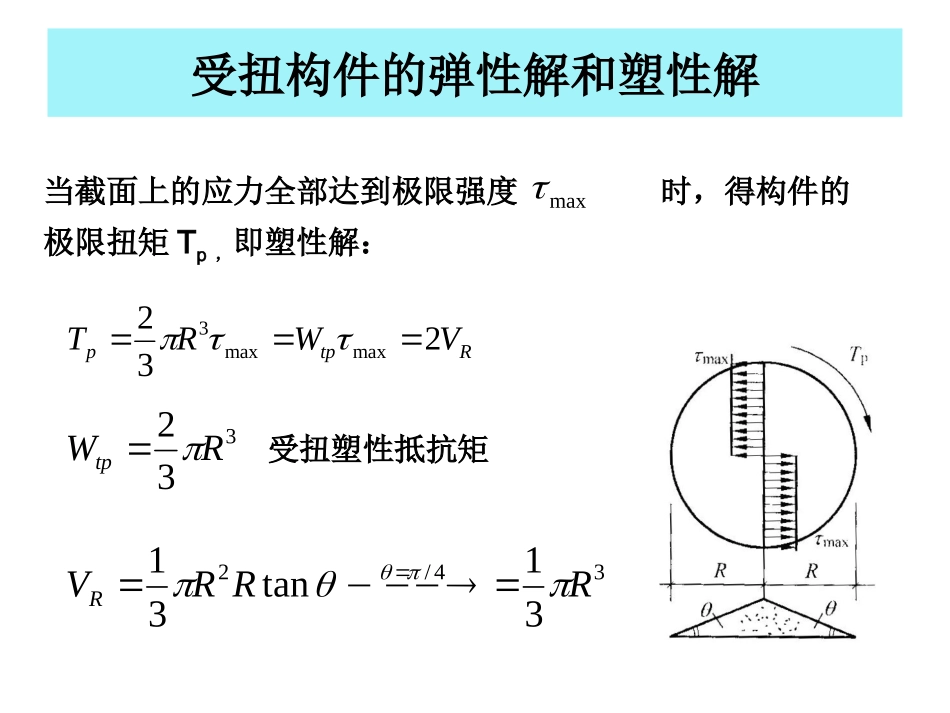
抗扭承载力受扭构件的弹性解和塑性解•弹性解0IrTe2/40RI其中-----截面的极惯性矩；当r=R时有最大剪应力：3max2RTe•圆形截面：e受扭构件的弹性解和塑性解tpW当截面上的应力全部达到极限强度时，得构件的极限扭矩Tp，即塑性解：maxRtppVWRT232maxmax334/231tan31RRRVR332RWtp受扭塑性抵抗矩受扭构件的弹性解和塑性解•矩形截面：teeeeWThbT2maxhbWete2bhptppVhbWbhbT2)3(61max2maxmax26)/(3hbp)3(612bhbWtpbhV当截面上的应力全部达到极限强度时，得构件的极限扭矩Tpmax塑性解：弹性解：为取决于截面边长比的受扭抵抗系数矩形截面的系数受扭构件的弹性解和塑性解0yxzyzx222pzyzxyFpzx对于一般情况，由弹塑性力学知纯扭问题满足平衡方程:假设材料服从Mises屈服条件，则有：定义应力函数Fp(x,y)，则有：xFpzypppgradFFppnF或则平衡方程自动满足，屈服条件变为受扭构件的弹性解和塑性解可以证明应力函数具有如下性质:在柱体表面上Fp(x,y)为常数，对于单连通截面Fp(x,y)lЃ=0。Fp(x,y)的等值线为剪应力迹线，即剪应力τ沿Fp(x,y)的等值线的切线方向。塑性应力曲面z=Fp(x,y)是等倾面，它的斜率就等于剪切屈服应力τp。利用砂堆曲面高程z1与塑性应力函数Fp(x,y)之间的比拟关系),(tan1yxFzpp受扭构件的弹性解和塑性解则柱体端面上的边界平衡条件可以写成：xypAppApApppAppzxAzypVdxdyFdxdyylxlFdxdyFdxdyFyyFxxFdxdyyFyxFxdxdyyxTtan22)(22)()()(21式中：θ为干砂的内摩擦角，Vxy为砂堆的体积。可见，塑性极限扭矩Tp与砂堆的体积Vxy成正比堆砂模拟法的结果制作一个与构件截面形状相同的平面，用松散的干燥细砂从其上均匀地撒下，直至砂粒从四周滚落，不能再往上堆积为止，最终的砂堆形状为锥形或坡形，取砂堆的倾斜率tanθ为塑性极限剪应力Rhtan1）横截面内各点剪应力大小相等(极限剪应力状态τmax)，且方向都与截面的周界平行；当周界有凹角时，剪应力迹线以圆弧线绕过尖角。2）对一般截面，砂堆会出现尖顶或棱线，在横截面上与这些点和线对应的两侧，剪应力不连续，即剪应力的方向发生跳跃式变化。圆形截面杆堆砂模拟法的结果hRVR231Rhtan利用砂堆比拟法求圆轴杆的塑性极限扭矩本问题的塑性应力曲面Z=Fp(x,y)是一个圆锥面。高圆锥高度为h，则砂堆的体积为：圆锥的坡度为：极限扭矩：ppRT332堆砂模拟法的结果•矩形截面杆：ba2tan堆砂的体积：)3(6)231(2)(21bhababbbabhVbh•四面坡屋顶曲面的最大坡度为：堆砂模拟法的结果•矩形截面杆：bhppVbhbT2)3(612正方形截面：pphT331狭长矩形截面：pphbT231开口薄壁截面：iniipphbT1221堆砂模拟法的近似计算•将截面分作若干个矩形块（bi×hi）的组合，按每块矩形的边长分别计算受扭塑性抵抗矩Wtpi,叠加后即得总塑性抵抗矩的近似值iniipitphbW12近似值与精确解的差别只在于矩形块相交的局部，且近似计算的砂堆体积总是偏小，即近似计算结果偏于安全。截面形状复杂的构件，可划分成不同的矩形块组合，应该选取抵抗矩有最大值的划分方法，一般的做法是首先满足截面上较宽部分的完整性。堆砂模拟法近似计算堆砂模拟近似计算的结果对于封闭的箱形截面构件，扭矩作用下的截面剪应力流方向一致，塑性抵抗矩很大。若将截面划分成矩形块，相当于把剪应力流限制在各矩形面积范围内，沿内壁的剪应力方向相反，内部自行抵消，使塑性抵抗矩远小于截面的应有值，误差过大，不宜采用。当t≥b/4时，可按实心截面计算；当t≤b/10时，壁板易压屈，不宜采用。纯扭构件的承载力无腹筋构件pptputeeTWTWTmax实验得矩形截面梁的极限扭矩：显然：ttpufWT)8.0~7.0(ttpefWT)667.0~590.0(3.1~1.1/euTT纯扭构件的承载力有腹筋构件ab正交于cdBc缝受拉，则da缝受压纯扭构件的承载力有腹筋构件...