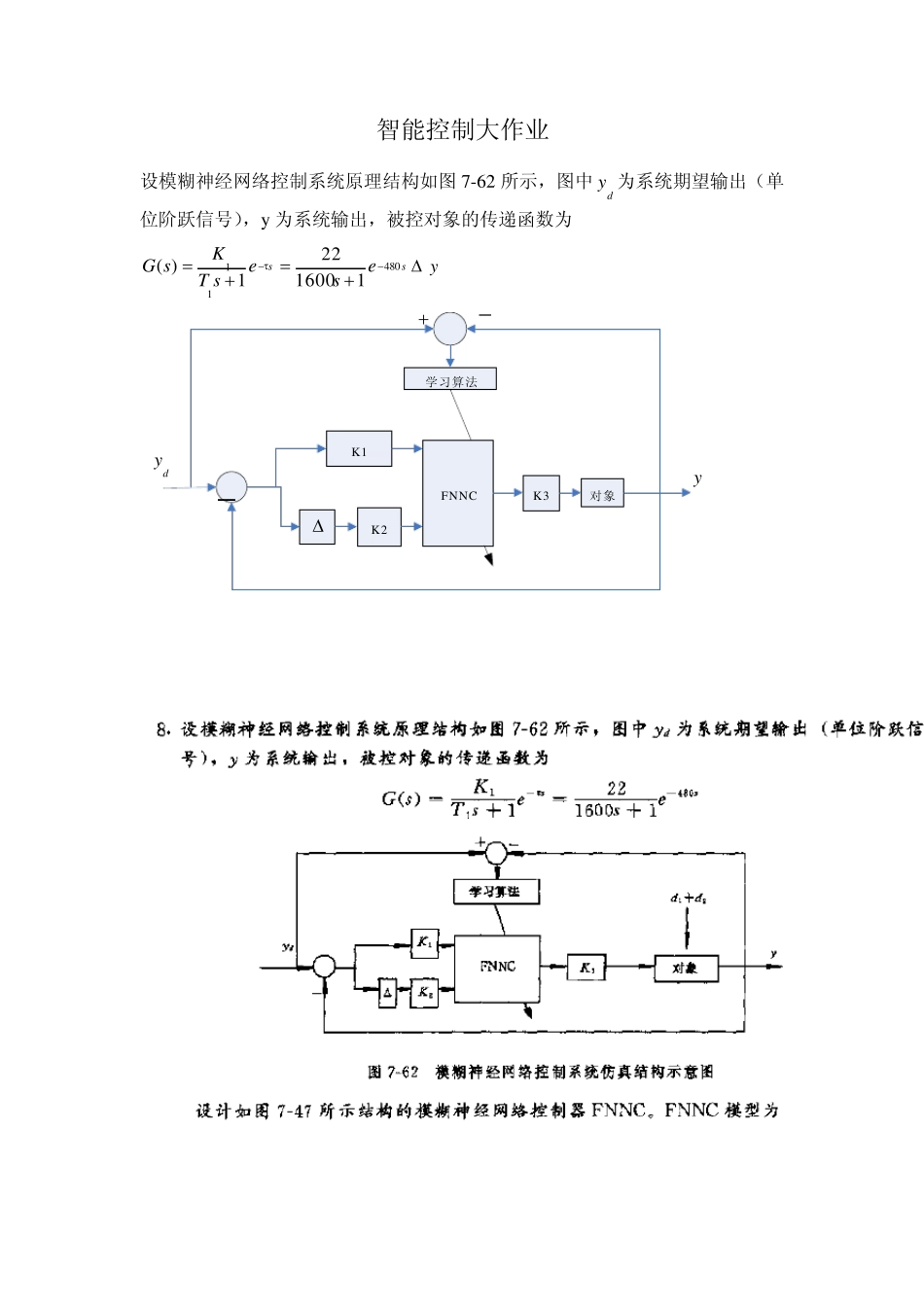
智能控制大作业 设模糊神经网络控制系统原理结构如图 7-62 所示,图中dy 为系统期望输出(单位阶跃信号),y为系统输出,被控对象的传递函数为 ssesesTKsG4801111600221)( y K2K3对象K1学习算法FNNC__dyy 解: 连续模型离散化 %工作的第一步:连续模型离散化 clear all close all H = tf([0 22],[1600 1],'inpu tdelay ',480) %得到 G(s) Hd = c2d(H,1,'foh') 程序运行结果: Transfer fu nction: 22 ex p(-480*s) * ---------- 1600 s + 1 MATLAB Transfer function: 0.006874 z + 0.006872 %将G(s)离散化 z^(-480) * --------------------- z - 0.9994 Sampling time: 1 因为: T0=1,T1=1600, =480,K1=22, 由计算可得: m=480,a1=0.9994,b1=0.006872 所以被控对象仿真模型可表示为: y(k+1)=0.9994y(k)+0.006872u(k-480-1)+d1+d2 令 d1=0.5sin(0.0314k),d2=0.5random(1)。 一、模糊神经网络理论 径向基函数(Radial Basis Function,RBF)神经网络是由J.Moody 和 C.Darken于 20 世纪 80 年代末提出的一种神经网络,它是具有单隐层的 3 层前馈网络。 RBF 中的作用函数是高斯基函数,其值在输入空间中有限范围内为非零值,因而 RBF 网络是局部逼近的网络。 1)RBF 网络的逼近 在 RBF 结构中,X=[x1,x2,...,xn]T 为网络的输入向量。 设 RBF 网络的径向基向量 H=[h1,h2,...,hm]T, 其中 hj 为高斯基函数,即 hj=exp(-||X-Cj||^2/(2*bj^2)), j=1,2,.....,m 式中,网络第 j 个节点的中心向量为 Cj=[cj1,cj2,....,cjn]T, i=1,2,...,n 设网络的基宽向量为 B=[b1,b2,....,bm]T bj 为节点 j 的基宽参数,且为大于零的数。 网络的权向量为 W=[w1,w2,...,wm] T RBF 网络的输出为 ym(k)=w1*h1+w2*h2+....+wm*hm RBF 网络逼近的性能指标函数为 E(k)=(y(k)-ym(k))^2/2 根据梯度下降法,输出权、节点基宽参数及节点中心矢量的迭代算法如下 wj(k)=wj(k-1)+η(y(k)-ym(k))hj+α*(wj(k-1)-wj(k-2)) △bj=(y(k)-ym(k))wj*hj*(||X-Cj||^2/(bj^3)) bj(k)=bj(k-1)+η△bj+α*(bj(k-1)-bj(k-2)) △cji=(y(k)-ym(k))wj*(xi-cji)/(bj^2) cji(k)=cji(k-1)+η△cji+α*(cji(k-1)-cji(k-2)) 式中,η 为学习速率,α 为动量因子,ηЄ[0,1],αЄ[0,1]。 2)高级神经网络 模糊 RBF 网络 在模糊系统中,模糊集,隶属...