最优控制讲义

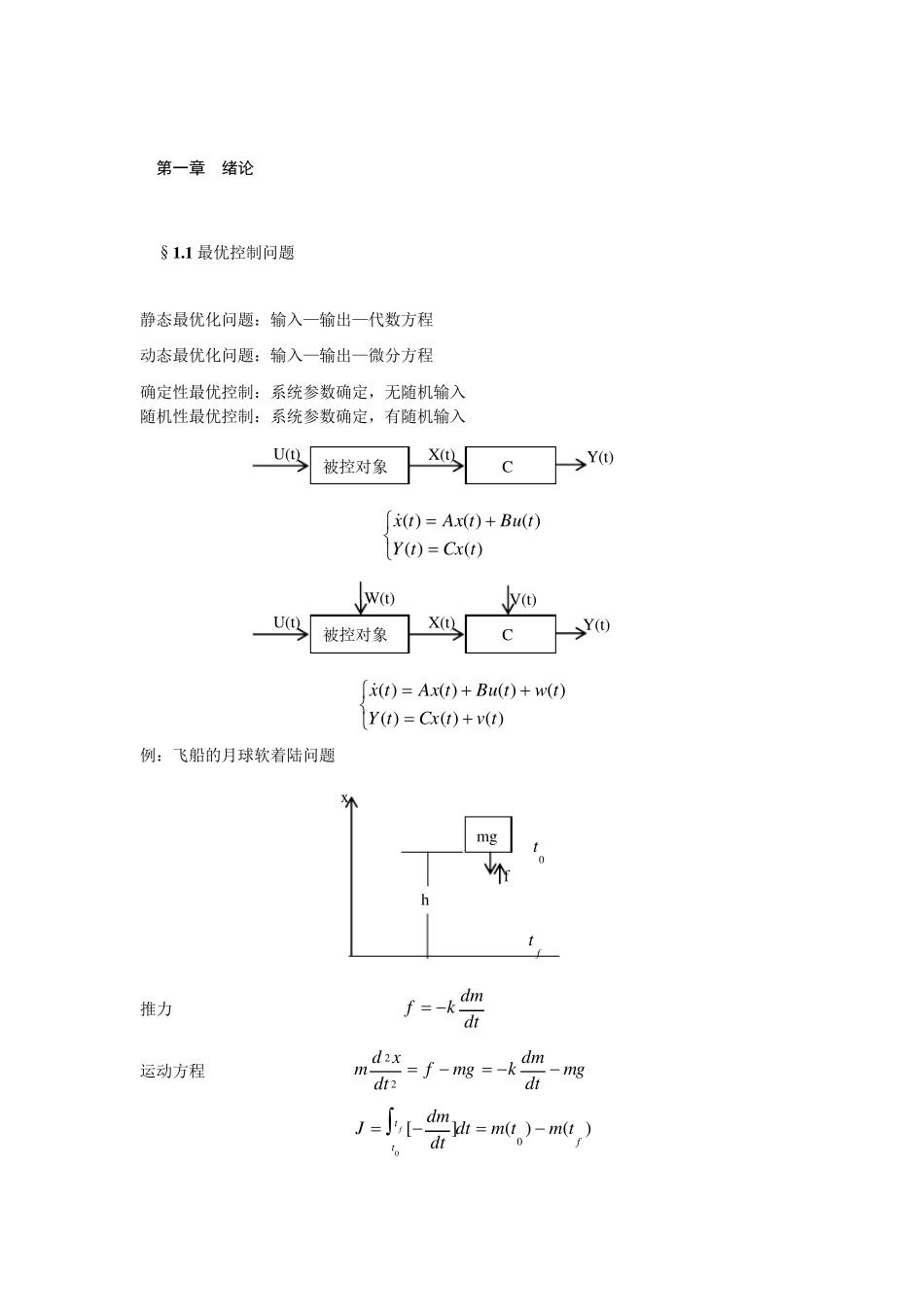
第一章 绪论 §1 .1 最优控制问题 静态最优化问题：输入—输出—代数方程 动态最优化问题：输入—输出—微分方程 确定性最优控制：系统参数确定，无随机输入 随机性最优控制：系统参数确定，有随机输入 )()()()()(tCxtYtButAxtx )()()()()()()(tvtCxtYtwtButAxtx 例：飞船的月球软着陆问题 推力 dtdmkf 运动方程 mgdtdmkmgfdtxdm22 )()(][00ftttmtmdtdtdmJf  被控对象 C U(t) X(t) Y(t) W(t) V(t) 被控对象 C U(t) X(t) Y(t) mg h x 0t ft f 初始条件 0)(,)(,00fftxxtthtxxtt 约束条件为 0dtdm 求minJ §1.2最优控制的数学模型 一 控制系统的数学模型(集中参数系统) 直接法建立：动力学、运动学的基本定律，即解析法. 间接法建立：通过“辩识”的途径确定系统的结构与参数. )),(),(()(ttutxftx 其 中 Tn txtxtxtx)](,)(),([)(21,Tr tutututu)](,)(),([)(21,],,[21nffff )(tx为n 维状态向量,)(tu为r 维控制向量, f 为n 维函数向量. 二 目标集 通过)(tu使)(tx由)(0tx到)(ftx，其中)(0tx为初始状态，并且通常为已知；)(ftx为终端状态，即控制所要求达到的目标。一般来说对终端状态的要求可用如下的约束条件表示：0)),((,0)),((21ffffttxgttxg. 三 容许控制 iu 具有不同的物理属性，一般有r1,2iui,,  ，即在控制域U 内.凡在闭区间],[0ftt上有定义，且控制域U 内取值的每一个控制函数)(tu均称为容许控制。 四 性能指标 主要取决于问题所要解决的主要矛盾。 表达式为： fttffdttuxLttxSuJ0),,()),(()]([ 其中)(tx是动态系统起始于00)(xtx，对应于)(tu的状态轨线。)(ftx是此轨线在终端时刻的值。 五 最优控制的提法 受控系统的状态方程及给定的初态 00 )(),),(),(()(ttxttutxftx 规定的目标集为 }0)),((,0)),((,)(:)({11ffffnffttxgttxgRtxtxM 求一容许控制],[,)(0ftttUtu，使指标函数 fttffdtttutxLttxSuJ0)),(),(()),(()]([ 为最小。 如果问题有解，记为)(* tu，则称)(* tu为最优控制。相应的曲线)(* tx叫做最优轨线。而性能指标)]([ **uJJ则称为最优性能指标。 §1.3 最优控制在实际问题应用的几个方程 一 时间最优控制 二 线性调节的问题 使线性系统的状态保持在平衡位置状态的误差最小，控...