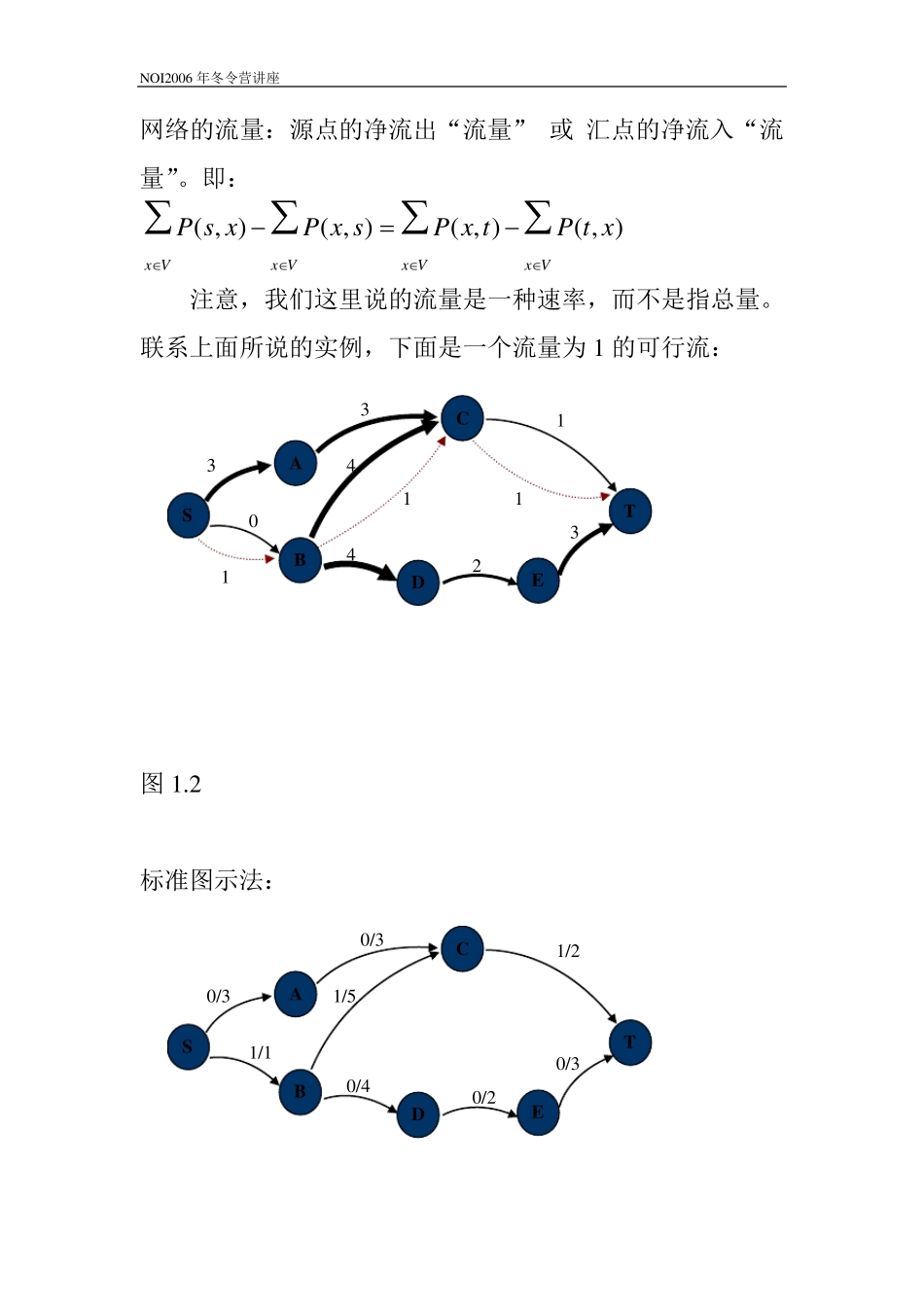
N O I2006 年冬令营讲座 最大流在信息学竞赛中应用的一个模型 江 涛 关键字: 网络 可行流 最大流 附加网络 无源汇 必要弧 流的分离 有上下界的最大流 建模 引言: 最大流类的模型在当今信息学比赛中有相当广泛的应用。但在教学中,发现很多同学对流模型的原理和变形并不掌握,只是记下经典的算法和题目,以便比赛中套用。 这当然有很大的局限性,也不是学习之正道。本讲想通过对最大流模型,特别是附加网络的一些分析、讨论,达到抛砖引玉目的。 一、网络与流的概念 一个实例:运输网络 D 3 S A B C T E 3 2 1 4 2 3 5 NOI2006 年冬令营讲座 图1.1 网络定义: 一个有向图 G=(V,E); 有两个特别的点:源点s、汇点t; 图中每条边(u,v)∈E,有一个非负值的容量C(u,v) 记为 G=(V,E,C) 网络三要素:点、边、容量 可行流定义: 是网络G 上的一个“流”,即每条边上有个“流量”P(u,v),要满足下面两个条件: 流的容量限制---弧: ),(),(0vuCvuP 对任意弧(u,v)---有向边 流的平衡---点: 除源点和汇点,对任意中间点有:流入 u 的“流量”与流出 u 的“流量”相等。即: },{ tsVu 有 VxVxxuPuxP0),(),( N O I2006 年冬令营讲座 网络的流量:源点的净流出“流量” 或 汇点的净流入“流量”。即: VxVxVxVxxtPtxPsxPxsP),(),(),(),( 注意,我们这里说的流量是一种速率,而不是指总量。联系上面所说的实例,下面是一个流量为 1 的可行流: 图 1.2 标准图示法: D 3 S A B C T E 3 1 0 4 2 3 4 1 1 1 D 0/3 S A B C T E 0/3 1/2 1/1 0/4 0/2 0/3 1/5 NOI2006 年冬令营讲座 图1.3 例1 .1 有一个n*m 的国际棋盘,上面有一些格子被挖掉,即不能放棋子,现求最多能放多少个棋子“车”,并保证它们不互相攻击(即:不在同一行,也不在同一列)? 分析: 1) 行、列限制---最多只能一个车控制; 2) 车对行、列的影响---一个车控制一个行和边; 例子: 图1.4 N O I2006 年冬令营讲座 图1.5 显然,我们要求车最多,也就是求流量最大---最大流问题。下面是一个解: 图1.6 即(1,3)、(2,1)、(3,2)格上各放一个车,可得到一个最优方案。 1 2 3 1 2 3 s t 1 1 1 1 1 1 1 2 3 1 2 3 s t 1 1 1 1 1 1 N O I2006 年冬令营讲座 二、最大流...