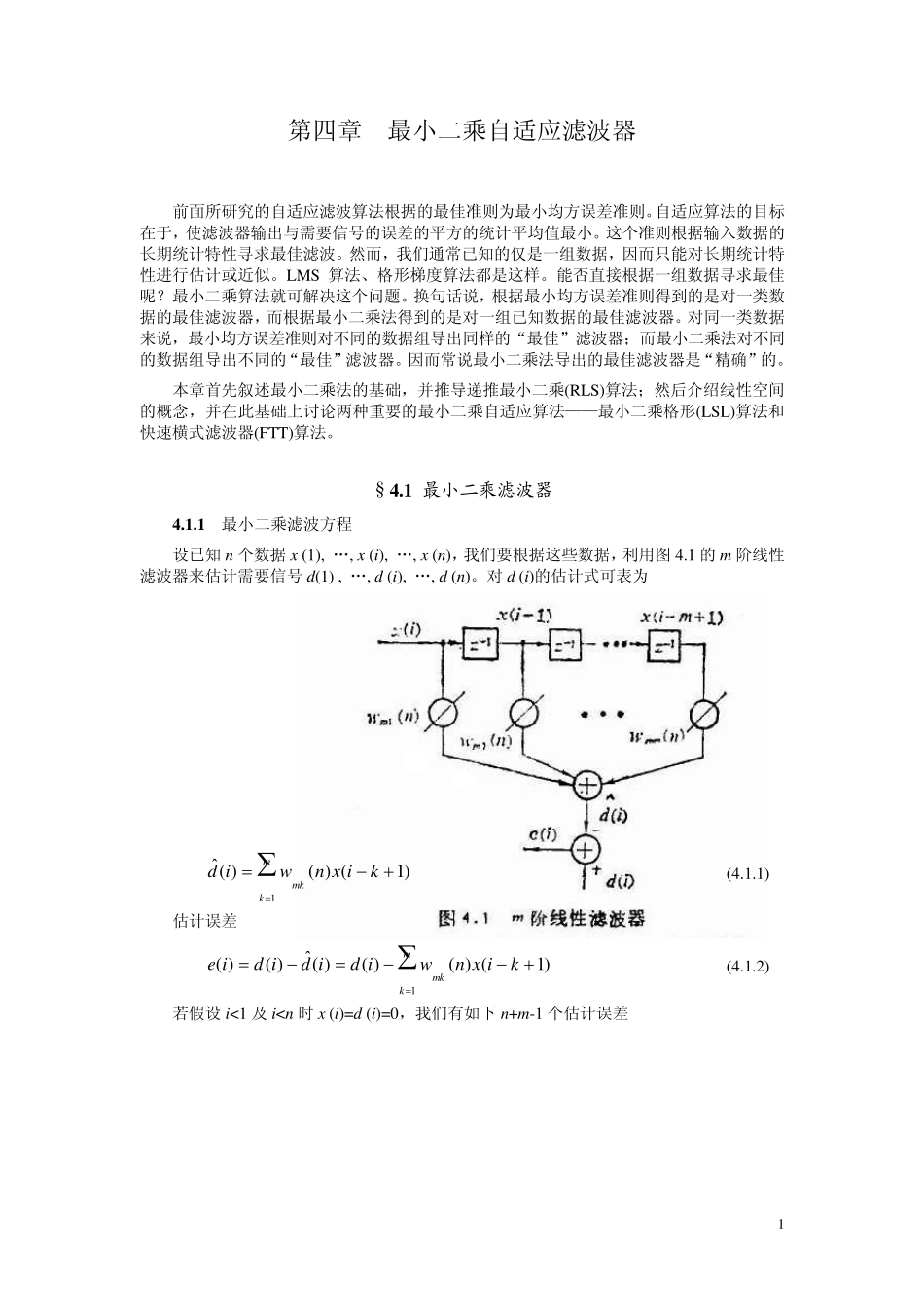
1 第四章 最小二乘自适应滤波器 前面所研究的自适应滤波算法根据的最佳准则为最小均方误差准则。自适应算法的目标在于,使滤波器输出与需要信号的误差的平方的统计平均值最小。这个准则根据输入数据的长期统计特性寻求最佳滤波。然而,我们通常已知的仅是一组数据,因而只能对长期统计特性进行估计或近似。LMS 算法、格形梯度算法都是这样。能否直接根据一组数据寻求最佳呢?最小二乘算法就可解决这个问题。换句话说,根据最小均方误差准则得到的是对一类数据的最佳滤波器,而根据最小二乘法得到的是对一组已知数据的最佳滤波器。对同一类数据来说,最小均方误差准则对不同的数据组导出同样的“最佳”滤波器;而最小二乘法对不同的数据组导出不同的“最佳”滤波器。因而常说最小二乘法导出的最佳滤波器是“精确”的。 本章首先叙述最小二乘法的基础,并推导递推最小二乘(RLS)算法;然后介绍线性空间的概念,并在此基础上讨论两种重要的最小二乘自适应算法——最小二乘格形(LSL)算法和快速横式滤波器(FTT)算法。 §4 .1 最小二乘滤波器 4 .1 .1 最小二乘滤波方程 设已知 n 个数据 x (1), „, x (i), „, x (n),我们要根据这些数据,利用图 4.1 的 m 阶线性滤波器来估计需要信号 d(1) , „, d (i), „, d (n)。对 d (i)的估计式可表为 mkmkkixnwid1)1()()(ˆ (4.1.1) 估计误差 mkmkkixnwidididie1)1()()()(ˆ)()( (4.1.2) 若假设 i<1 及 in 时...