医学统计学列联表检验VIP免费

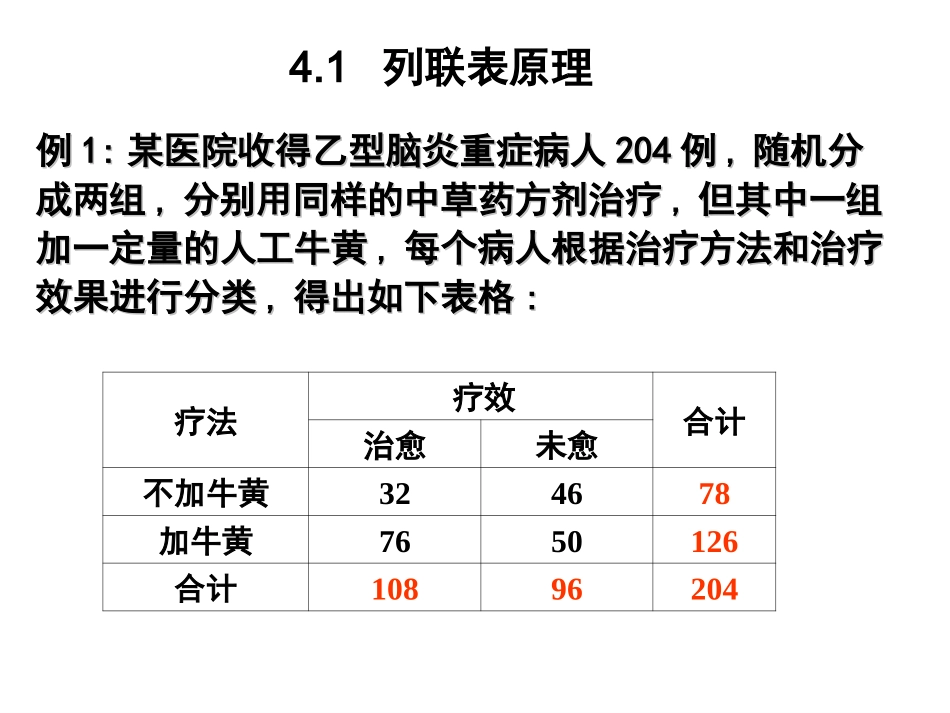
第四章列联表分析4.1列联表原理4.2Crosstabs过程例例1:1:某医院收得乙型脑炎重症病人某医院收得乙型脑炎重症病人204204例例,,随机分随机分成两组成两组,,分别用同样的中草药方剂治疗分别用同样的中草药方剂治疗,,但其中一组但其中一组加一定量的人工牛黄加一定量的人工牛黄,,每个病人根据治疗方法和治疗每个病人根据治疗方法和治疗效果进行分类效果进行分类,,得出如下表格得出如下表格::4.1列联表原理疗法疗效合计治愈未愈不加牛黄324678加牛黄7650126合计10896204列联表列联表：：观测数据按两个或更多属性（定性变量）分类观测数据按两个或更多属性（定性变量）分类时所列出的频数表。时所列出的频数表。R×CR×C列联表列联表：分类频数排成：分类频数排成RR行行CC列的列联表。列的列联表。2×22×2表表：二行二列的列联表，又称：二行二列的列联表，又称四格表四格表。。列联表分析：使用列联表进行分类资料的检验。列联表分析：使用列联表进行分类资料的检验。※※双向无序双向无序单向有序单向有序双向有序且属性不同双向有序且属性不同列联表列联表双向有序且属性相同双向有序且属性相同设不加牛黄组治愈总体率为，加牛黄组治愈总体率为设不加牛黄组治愈总体率为，加牛黄组治愈总体率为检验检验即即““疗法”与“疗效”独立疗法”与“疗效”独立1.双向无序表独立性检验双向无序列联表：两个分类变量分类标志无数值大小两个分类变量分类标志无数值大小与先后顺序之分。与先后顺序之分。疗法疗效合计治愈未愈不加牛黄324678加牛黄7650126合计10896204CRjijiijOOON,1,221(1)(1)dfRC22()df若0H拒绝H0：X与Y独立（即两组总体率相同）实际频数Oij与理论频数Eij的差异是随机误差,用Pearson卡方统计量反映实际Oij与理论Eij吻合程度..ijijOOEN注意：上述检验适用于双向无序的表注意：上述检验适用于双向无序的表(df(df≠1)≠1)分组标志无数量大小和先后顺序之分。分组标志无数量大小和先后顺序之分。分析的目的是考察两个属性之间是否独立分析的目的是考察两个属性之间是否独立。。疗效疗法中医西医痊愈显效合计687372638835好转无效15251121155注：2.若R×C列联表中理论频数出现小于1，或理论频数出现小于5的格数超过总格数1/5时，必须增大样本例数;或把理论频数太小的行,列与性质相近的邻行,列合并;或删去理论频数太小的行,列。最小理论频数=最小行合计频数﹒最小列合计频数/总频数1.双向无序列联表计算卡方统计量常用单侧检验。3.多个总体率比较的卡方检验，若结论为拒绝原假设，只能认为总体率之间不全等，不能说明任意两个总体率有无差别，需做多重比较。例：判断患鼻咽癌与血型有无关系分类A型血B型血O型血AB型血合计患癌者648613020300健康人12513821026499合计18922434046799第一行合计数,第四列合计数最小,最小理论频数143004617.275799EH0:“患癌”与“血型”独立,H1:“患癌”与“血型”不独立df＝(2－1)(4－1)＝3，单侧概率P>0.05，不能以α＝0.05水准的单侧检验拒绝H0，总体率的差异无统计意义,不能认为患鼻咽癌与血型不独立。222,2,12220.056486(1)7993001893002242102611.921(3)7.81549934049946RCijijijONOO2.四格表独立性检验例例1:1:某医院收得乙型脑炎重症病人某医院收得乙型脑炎重症病人204204例例,,随机分随机分成两组成两组,,分别用同样的中草药方剂治疗分别用同样的中草药方剂治疗,,但其中一组但其中一组加一定量的人工牛黄加一定量的人工牛黄,,每个病人根据治疗方法和治疗每个病人根据治疗方法和治疗效果进行分类效果进行分类,,得出如下表格得出如下表格::疗法疗效合计治愈未愈不加牛黄324678加牛黄7650126合计10896204双向无序四格表（1）N≥40，理论频数≥522,22,1()ijijijijOEE21212211222112)(OOOOOOOON（2）N≥40，理论频数小于5(但≥1)，用校正卡方统计量(3)N<40或理论频数小于1,不能使用卡方检验,应使用Fisher精确检验,称为四格表确切概率法。列联表的原假设是两个变量X和Y相互独立，计算卡方统计量，当...