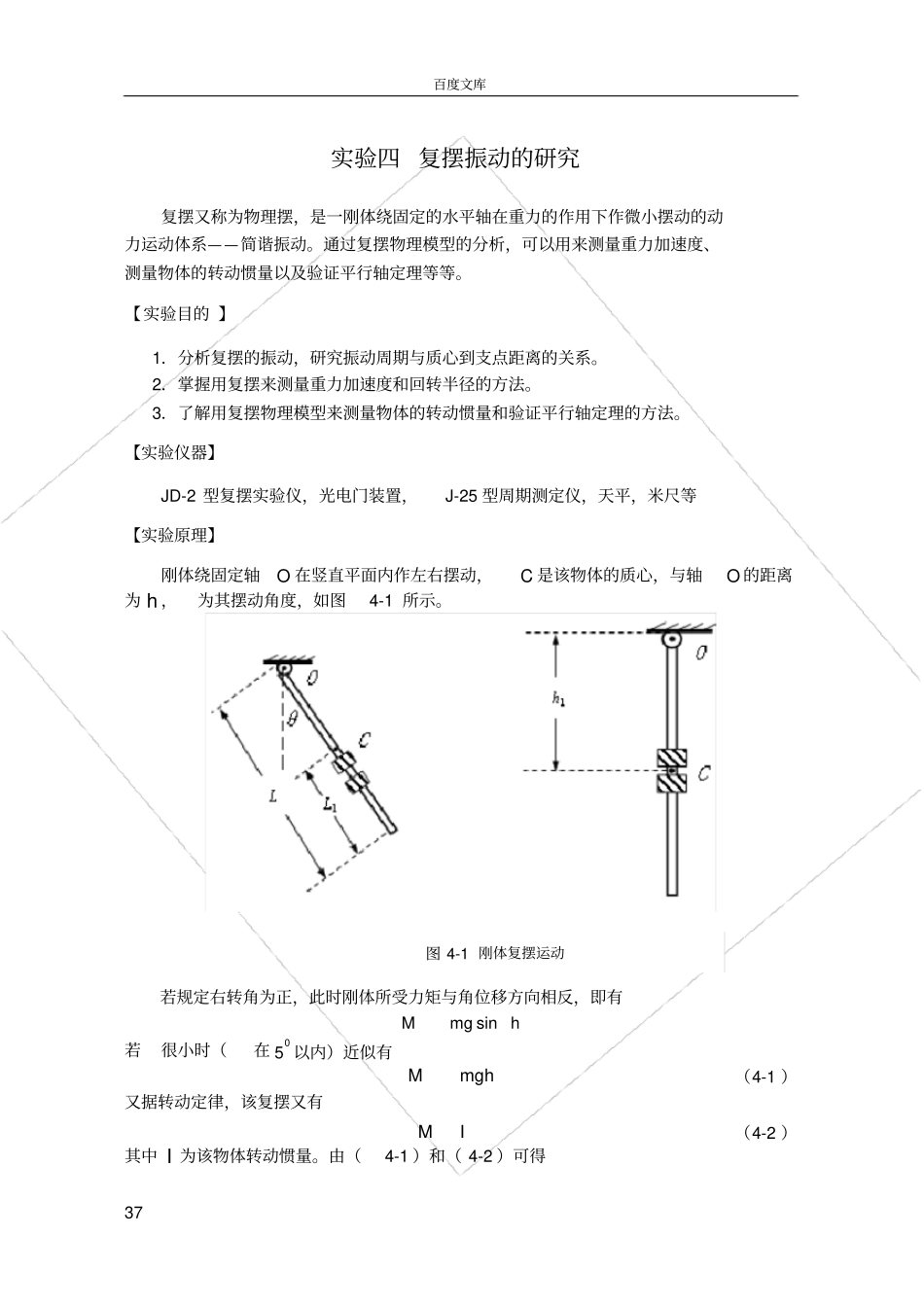
百度文库37 实验四 复摆振动的研究复摆又称为物理摆,是一刚体绕固定的水平轴在重力的作用下作微小摆动的动力运动体系——简谐振动。通过复摆物理模型的分析,可以用来测量重力加速度、测量物体的转动惯量以及验证平行轴定理等等。【实验目的 】1.分析复摆的振动,研究振动周期与质心到支点距离的关系。2.掌握用复摆来测量重力加速度和回转半径的方法。3.了解用复摆物理模型来测量物体的转动惯量和验证平行轴定理的方法。【实验仪器】JD-2 型复摆实验仪,光电门装置,J-25 型周期测定仪,天平,米尺等【实验原理】刚体绕固定轴O 在竖直平面内作左右摆动,C 是该物体的质心,与轴O 的距离为 h ,为其摆动角度,如图4-1 所示。若规定右转角为正,此时刚体所受力矩与角位移方向相反,即有hmgMsin若很小时(在05 以内)近似有mghM(4-1 )又据转动定律,该复摆又有IM(4-2 )其中 I 为该物体转动惯量。由(4-1 )和( 4-2 )可得图 4-1 刚体复摆运动百度文库38 20(4-3 )其中20mghI。此方程说明该复摆在小角度下作简谐振动,该复摆周期为mghIT2(4-4 )设cI 为转轴过质心且与O 轴平行时的转动惯量,那么根据平行轴定律可知2mhIIc(4-5 )代入 (4-4) 式得:mghmhITc22( 4-6 )由此可见,周期T 是质心到回转轴距离h 的函数,且当0h或 h时, T。因此,对下面的情况分别进行讨论:( 1) h 在零和无穷大之间必存在一个使复摆对该轴周期为最小的值,此时所对应 h值叫做 复摆的回转半径,用 R 表示。由( 4-6)式和极小值条件0dTdh得:mincTTIRhm(4-7)代入公式( 4-7)又得最小周期为min22RTg(4-8)( 2)在 hR两边必存在无限对回转轴,使得复摆绕每对回转轴的摆动周期相等。而把这样的一对回转轴称为共轭轴,假设某一对共轭轴分别到重心的距离为1h 、2h (12hh ),测其对应摆动周期为1T 、 2T 。将此数据分别代入 ( 4-6)式并利用12TT得:12cImh h(4-9)122hhTg(4-10)把公式(4-10)与单摆的周期公式2lTg比较可知, 复摆绕距的重心为1h(或其共轭轴2h )的回转轴的摆动周期与所有质量集中于离该轴为12hh 点的单摆周期百度文库39 相等,故称h1+h2 为该轴的 等值摆长 。可见,实验测出复摆的摆动周期T 及该轴的等值摆长 h1+h2,由公式( 4-10)就可求出当地的重力加速度g 的值。本实验所用复摆为一均匀钢板,它上面从中心向两端对称地开一些小孔。测量时分别将复摆通过小圆...