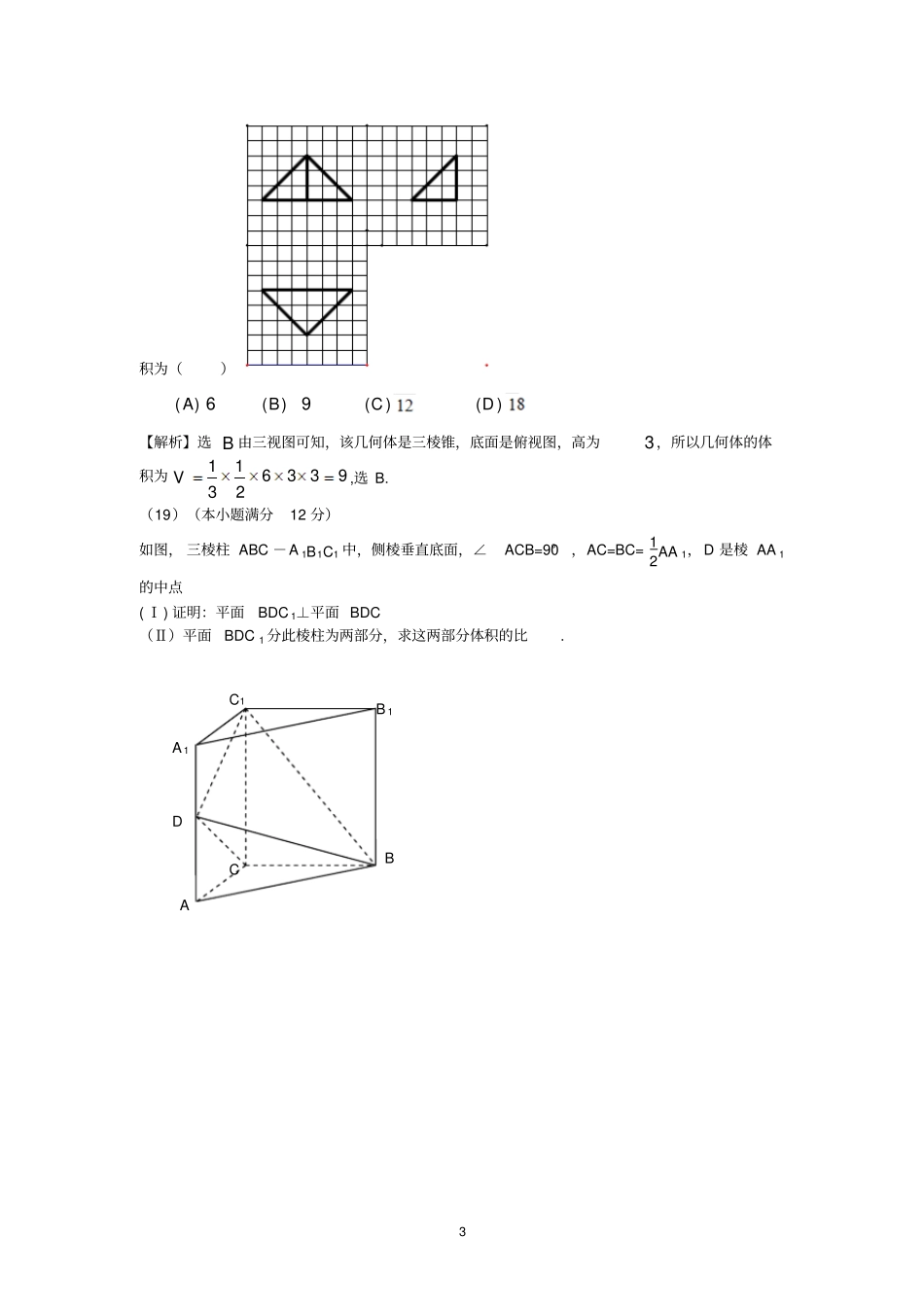
1 2011 年普通高等学校招生全国统一考试文科数学(8)在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的俯视图可以为 (D) (18)(本小题满分12 分)如图,四棱锥 PABCD 中,底面 ABCD 为平行四边形。60 ,2,DABABAD PD底面 ABCD 。(I )证明: PABD(II )设1PDAD,求棱锥 DPBC 的高。2 2012 年普通高等学校招生全国统一考试文科数学7.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体3 积为()()A 6()B9()C()D【解析】选 B 由三视图可知,该几何体是三棱锥,底面是俯视图,高为3,所以几何体的体积为93362131V,选 B. (19)(本小题满分12 分)如图, 三棱柱 ABC -A 1B1C1 中,侧棱垂直底面,∠ACB=90°,AC=BC= 12AA 1,D 是棱 AA 1的中点( I) 证明:平面BDC 1⊥平面 BDC(Ⅱ)平面BDC 1 分此棱柱为两部分,求这两部分体积的比. B 1C B A D C1A 14 2013 年普通高等学校招生全国统一考试(11)某几何函数的三视图如图所示,则该几何的体积为()(A )168(B)88(C)16 16(D)81619.(本小题满分12 分)如图,三棱柱111ABCA B C 中, CACB,1ABAA ,160BAA。(Ⅰ)证明:1ABA C ;(Ⅱ)若2ABCB,16AC,求三棱柱111ABCA B C 的C1B1AA1BC5 体积。2013 年普通高等学校招生全国统一考试(新课标Ⅱ卷 ) 9、一个四面体的顶点在空间直角坐标系Oxyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0) ,画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到正视图可以为()(A) (B) (C) (D) 【答案】 A 【解析】在空间直角坐标系中,先画出四面体OABC 的直观图,以zOx 平面为投影面,则得到正视图 (坐标系中红色部分),所以选 A. (15)已知正四棱锥OABCD 的体积为 3 22,底面边长为3 ,则以 O 为球心, OA 为半径的球的表面积为________。【答案】 246 【解析】设正四棱锥的高为h ,则213 2(3)32h,解得高3 22h。则底面正方形的对 角 线 长 为236 , 所 以223 26()()622OA,所 以 球 的 表 面 积 为24 ( 6)24. (18)如图,直三棱柱111ABCA B C 中, D , E 分别是 AB ,1BB 的中点,。(Ⅰ)证明:1 / /BC平面11A CD ;(Ⅱ)设12AAACCB,2 2AB,求三棱锥1CA DE 的体积。2014 年高招全国课标 1(文科数学 word 解析版)第Ⅰ卷8.如图,网格纸的各小格都是...