单纯形法基本原理及实例演示VIP免费

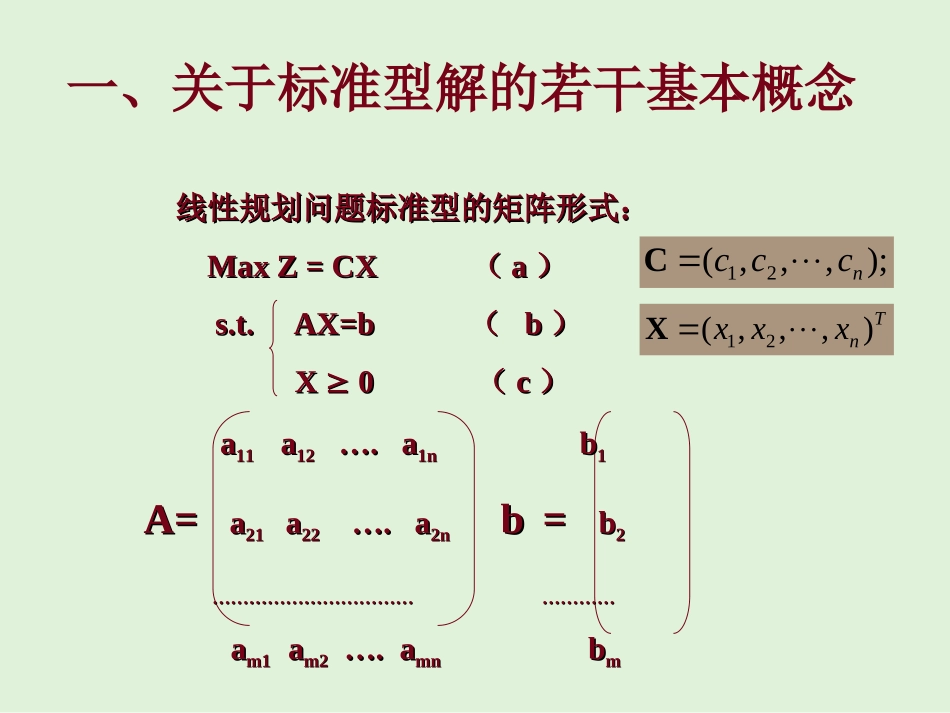
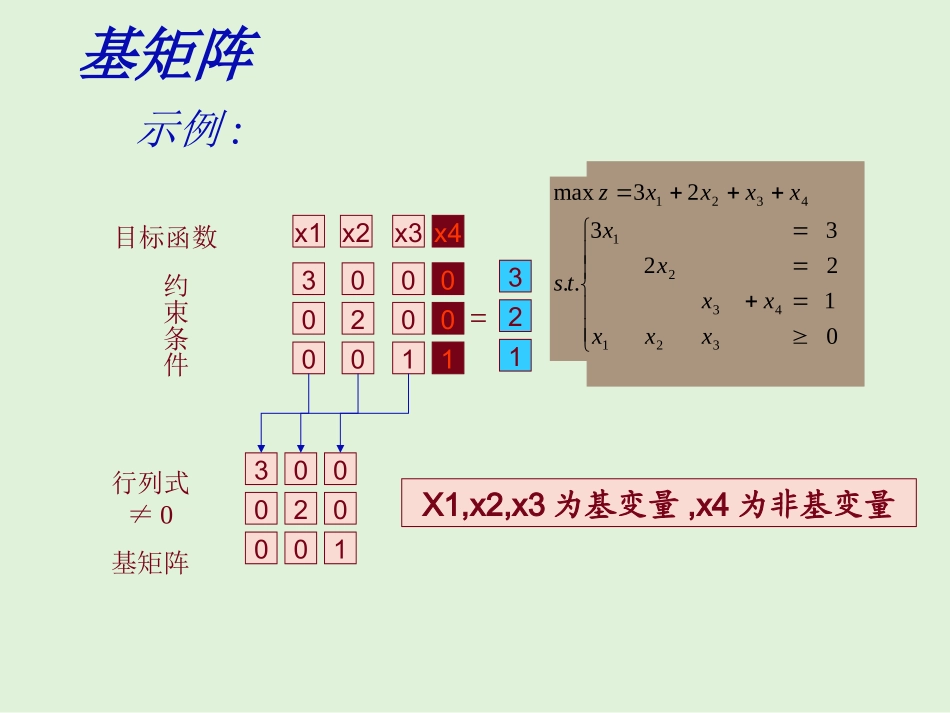
单纯形法求解—动态演示在求解LP问题时,有人给出了图解法,但对多维变量时,却无能为力,于是美国数学家G·B·Dantgig(丹捷格)发明了一种“单纯形法”的代数算法，尤其是方便于计算机运算。这是运筹学史上最辉煌的阶段。线性规划问题标准型的矩阵形式：线性规划问题标准型的矩阵形式：MaxZ=CXMaxZ=CX（（aa））s.t.AX=bs.t.AX=b（（bb））XX00（（cc））aa1111aa1212….a….a1n1nbb11A=A=aa2121aa2222….a….a2n2nbb==bb22………………………………………………………………………………aam1m1aam2m2….a….amnmnbbmm);,,,(21ncccCTnxxx),,,(21X一、关于标准型解的若干基本概念基矩阵示例:012233..23max32143214321xxxxxxxtsxxxxz000032020001010x1x2x4x3001300321=目标函数约束条件行列式≠0基矩阵X1,x2,x3为基变量,x4为非基变量因为因为BB为基为基,,故有故有XXBB+B+B-1-1NXNXNN=B=B-1-1bb，，解得可行解解得可行解XXBB=B=B-1-1b-Bb-B-1-1NXNXNN，，代入目标函数代入目标函数ZZ，，Z=Z=CCBBBB-1-1b+b+(C(CNN--CCBBBB-1-1N)N)XXNN令非基变量令非基变量XXNN=0=0，则有，则有XT=(XB,XN)T=（B-1b,0)TZ=CBB-1bAX=bAX=bZ=CXZ=CX设设A=A=（（B,NB,N）（）（BB为一个基，即线性无关向量组为一个基，即线性无关向量组R(A)=RR(A)=R(B)(B)））XXTT=(X=(XBB,X,XNN))TT（（XXBB为基变量，为基变量，XXNN为非基变量）为非基变量）C=(CC=(CBB,C,CNN))（（CCBB为基变量系数，为基变量系数，CCNN为非基变量系数）为非基变量系数）则有：则有：Z=Z=(C(CBB,C,CNN)(X)(XBB,X,XNN))TT=C=CBBXXBB+C+CNNXXNNAX=AX=（（B,NB,N））(X(XBB,X,XNN))TT=B=BXXBB+N+NXXNN=b=b11、单纯形法原理：、单纯形法原理：Z=Z=CCBBBB-1-1b+b+(C(CNN--CCBBBB-1-1N)N)XXNN如果如果CCNN--CCBBBB-1-1NN小于小于00，无论，无论XXNN取任何取任何大于大于00值，只会让值，只会让ZZ变小，因此我们可以通过变小，因此我们可以通过CCNN--CCBBBB-1-1NN来判断来判断ZZ取得是不取得是不是最大值。是最大值。如果存在一个如果存在一个CCNN--CCBBBB-1-1NN大于大于00，则说明，则说明ZZ的值会随着的值会随着XXNN增大而增大，说明增大而增大，说明ZZ有调整的余地。有调整的余地。定理一：若某个基本可行解所对应的检验向量定理一：若某个基本可行解所对应的检验向量CCNN--CCBBBB-1-1NN<=0,<=0,则这个基本可行解就是最优解。则这个基本可行解就是最优解。定理二定理二：：若某个基本可行解所对应的检验向量若某个基本可行解所对应的检验向量CCNN--CCBBBB-1-1NN存在一个检验数存在一个检验数=0,=0,则该问题有无数多个最优解。则该问题有无数多个最优解。定理三：若定理三：若某个基本可行解所对应的检验向量某个基本可行解所对应的检验向量CCjj--CCBBBB-1-1NNjj大大于于00，且，且aaijij,,都小于都小于00，则无解。，则无解。为了矩阵形求逆计算方便，一般将B转化为单位矩阵。①将线性规划问题化成标准型。②找出或构造一个m阶单位矩阵作为初始可行基，建立初始单纯形表。③计算各非基变量xj的检验数j=Cj-CBPj′，若所有j≤0，则问题已得到最优解，停止计算，否则转入下步。④在大于0的检验数中，若某个k所对应的系数列向量Pk≤0，则此问题是无界解，停止计算，否则转入下步。⑤根据max{j｜j＞0}=k原则，确定xk为换入变量(进基变量)，再按规则计算：=min{bi/aik|aik＞0}=bl/aik确定xBl为换出变量。建立新的单纯形表，此时基变量中xk取代了xBl的位置。⑥以aik为主元素进行迭代，把xk所对应的列向量变为单位列向量，即aik变为1，同列中其它元素为0，转第③步。2、单纯形法的计算步骤线性规划的例子0,40025005.2516002234max211212121xxxxxxxxxz线性规划--标准化引入变量：s1,s2,s3121231211222312123max501000003002400250,,,,0zxxsssxxsxxsxsxxsss25040030032121100100101200111sssxx3020102100150maxsssxxz•提取系数，填...