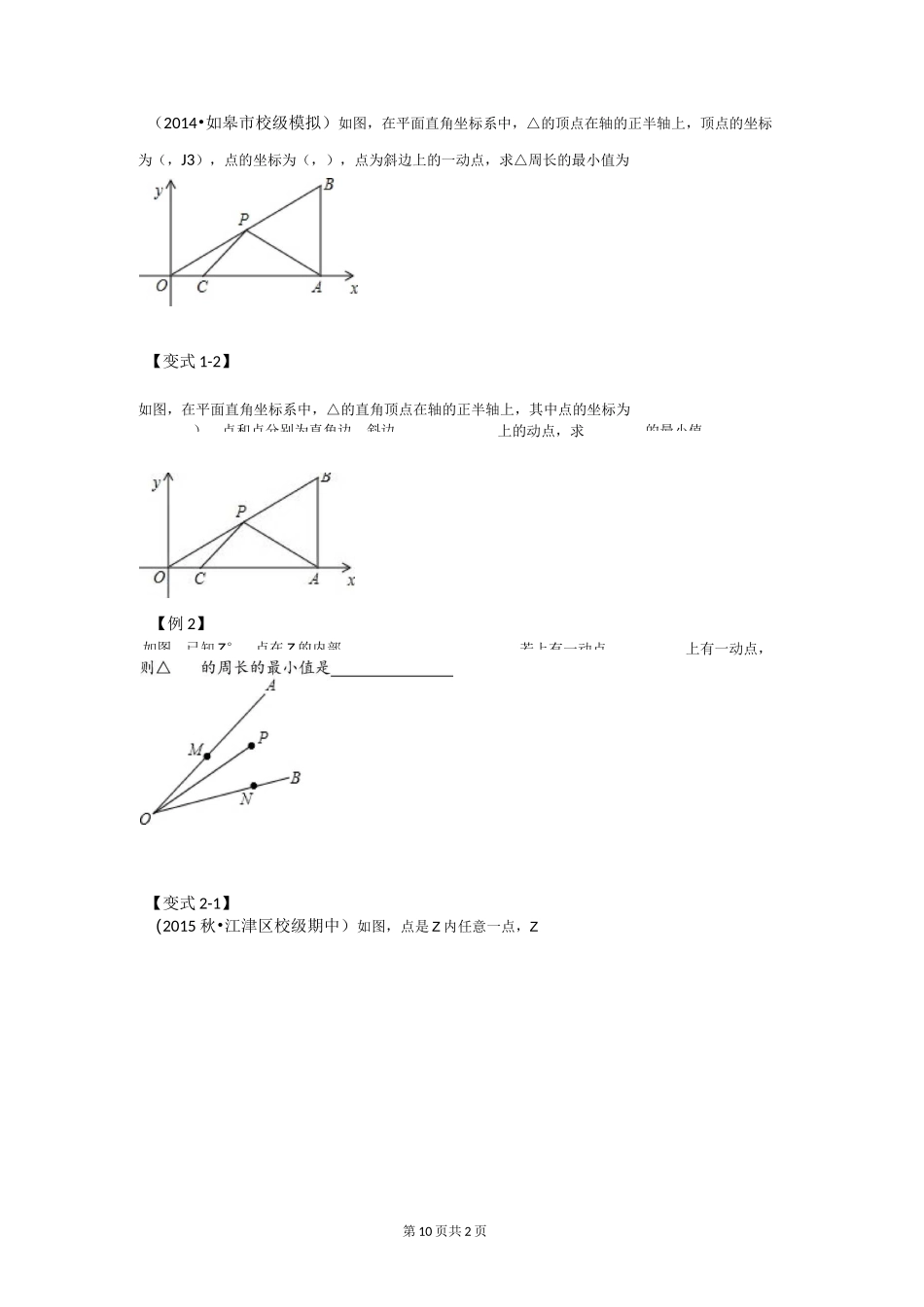
【变式 1-1】初中的几何最值问题解题策略几何中的最值问题,一直是个比较复杂的问题,多数同学在处理时思路不清晰的,下面我们从多年的解题经验中跟大家分享下我们的解题思路,碰到这种类型的问题应该如何解决。总结各种最值问题,无外乎考查的知识点不过是三个,不管是初二,初三,还是总复习都是如此。我们主要从接下来的三个知识点入手,那么这种几何最值问题都会有一定思路,解题起来相对简单许多。一、两点之间线段最短二、三边关系求最值(最大或最小)三、垂线段最短求最值接下来,我们逐个去介绍,并进行相关的练习,在练习中体会解决问题的思路,有时三个知识点也是共同使用的,不是单个解决的,这里需要我们总结思路,举一反三,触类旁通。(后面的题型丰富,题目较新,适合练习,大家务必认真练练,必有所获的)一、两点之间线段最短这个知识点的运用中,通常的解题步骤是:1、先作对称 2、用知识点 3、算结果。在作对称的过程中,一般都是作定点关于对称轴的对称点,然后带入知识点,两点之间线段最短直接找到最小值时的点的位置。这样思路就打开了。【例 1】如图,△的直角顶点在轴的正半轴上,Z°,(,2J3),(,),为上一动点.()若点关于直线的对称点为,求的坐标;()求出△周长的最小值.第 10 页共 2 页),点和点分别为直角边、斜边上的动点,求的最小值.【例 2】如图,已知 Z°,点在 Z 的内部,,若上有一动点上有一动点,(2014•如皋市校级模拟)如图,在平面直角坐标系中,△的顶点在轴的正半轴上,顶点的坐标为(,J3),点的坐标为(,),点为斜边上的一动点,求△周长的最小值为【变式 1-2】如图,在平面直角坐标系中,△的直角顶点在轴的正半轴上,其中点的坐标为【变式 2-1】(2015 秋•江津区校级期中)如图,点是 Z 内任意一点,Z第 10 页共 3 页上的动点,则△周长的最小值是和点分别是射线和射线第 10 页共 4 页【变式 2-2】(2015 秋•日照期末)如图,四边形中,Z°,乙乙°,、分别是、上的一点,当△的周长最小时,Z 的度数为.、三边关系求最值(最大或最小)关于这个知识点,我们要从两方面来思考,一是线段之和的最小值,比如的最小值是;另一方面是线段之差的最大值,比如例中的的最大值;有的时候我们还会碰到三个线段之和的最小值,其中一个线段的长是定值,那么这时我们一般都是通过平行四边形,把他们转化成普通的线段之和的最小值来解决,这样就比较简单了。【例 1】(春•泰兴市校级...