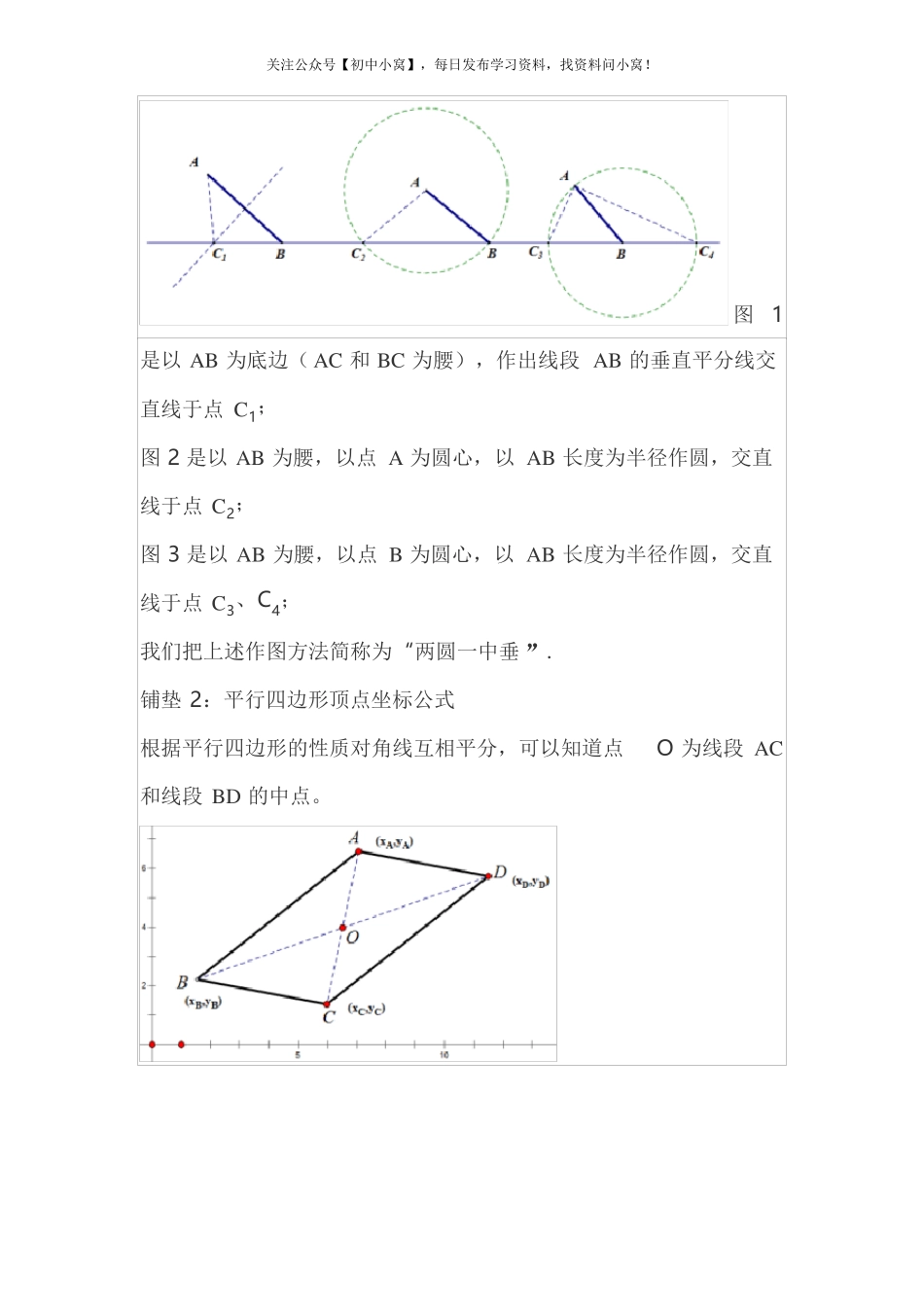
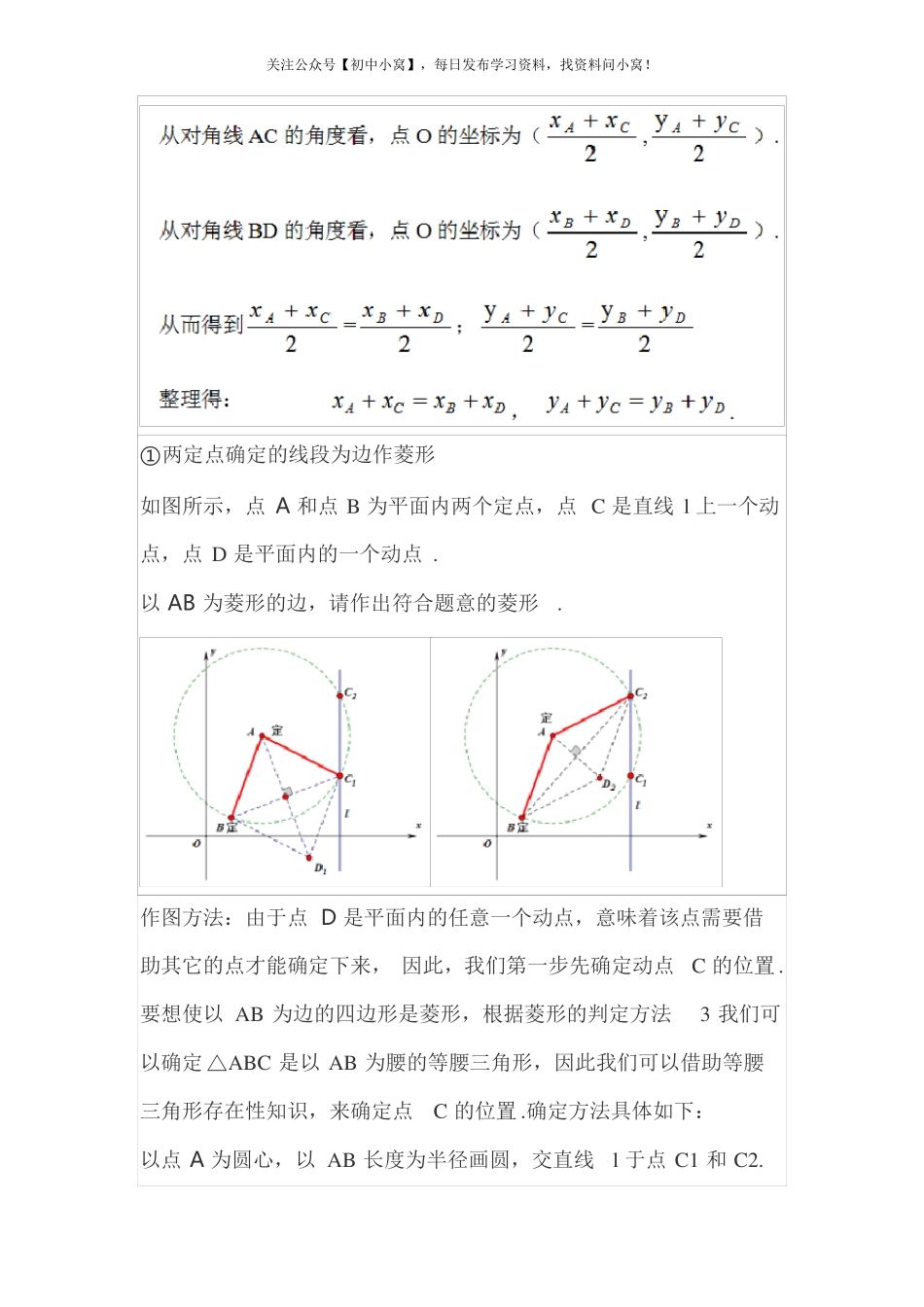
关注公众号【初中小窝】,每日发布学习资料,找资料问小窝!我们已经知道菱形是特殊的平行四边形, 它的判定方法一共有五种,分别是①四边都相等的四边形是菱形;②两条对角线互相垂直的平行四边形是菱形 ;③邻边相等的平行四边形是菱形; ④对角线互相垂直平分的四边形是菱形 ;⑤一条对角线平分一个顶角的平行四边形是菱形.在做几何证明题的时候我们常用的判定方法主要是前三种.二次函数和菱形存在性问题作为压轴题目,结合了“分类讨论思想”,“方程思想”“菱形的判定方法”,势必要比单纯的菱形判定思考难度要大的多,因此我在研究了近些年中考真题之后尝试性的总结一下菱形存在性问题的通用解法,以供大家参考.纵观历年中考真题,菱形存在性问题主要是以“两定两动”为设问方式,其中两定指的是四边形四个顶点其中有两个顶点的坐标是确定的或者是可求解的;两动指的是其中一个动点在一条直线或者抛物线上,另外一个动点是平面内任意一点或者该动点也在一条直线或者抛物线上.一 解题模型铺垫 1:等腰三角形的构造方法点 A 和点 B 为平面内的两个定点,点C 为水平直线上的一个动点,要使△ABC 为等腰三角形,请利用尺规作图的方法作出点C 的位置 .关注公众号【初中小窝】,每日发布学习资料,找资料问小窝!图1是以 AB 为底边( AC 和 BC 为腰),作出线段 AB 的垂直平分线交直线于点 C1;图 2 是以 AB 为腰,以点 A 为圆心,以 AB 长度为半径作圆,交直线于点 C2;图 3 是以 AB 为腰,以点 B 为圆心,以 AB 长度为半径作圆,交直线于点 C3、C4;我们把上述作图方法简称为 “两圆一中垂 ”.铺垫 2:平行四边形顶点坐标公式根据平行四边形的性质对角线互相平分,可以知道点O 为线段 AC和线段 BD 的中点。关注公众号【初中小窝】,每日发布学习资料,找资料问小窝!①两定点确定的线段为边作菱形如图所示,点 A 和点 B 为平面内两个定点,点 C 是直线 l 上一个动点,点 D 是平面内的一个动点 .以 AB 为菱形的边,请作出符合题意的菱形.作图方法:由于点 D 是平面内的任意一个动点,意味着该点需要借助其它的点才能确定下来, 因此,我们第一步先确定动点C 的位置 .要想使以 AB 为边的四边形是菱形,根据菱形的判定方法3 我们可以确定 △ABC 是以 AB 为腰的等腰三角形,因此我们可以借助等腰三角形存在性知识,来确定点C 的位置 .确定方法具体如下:以点 A 为圆...