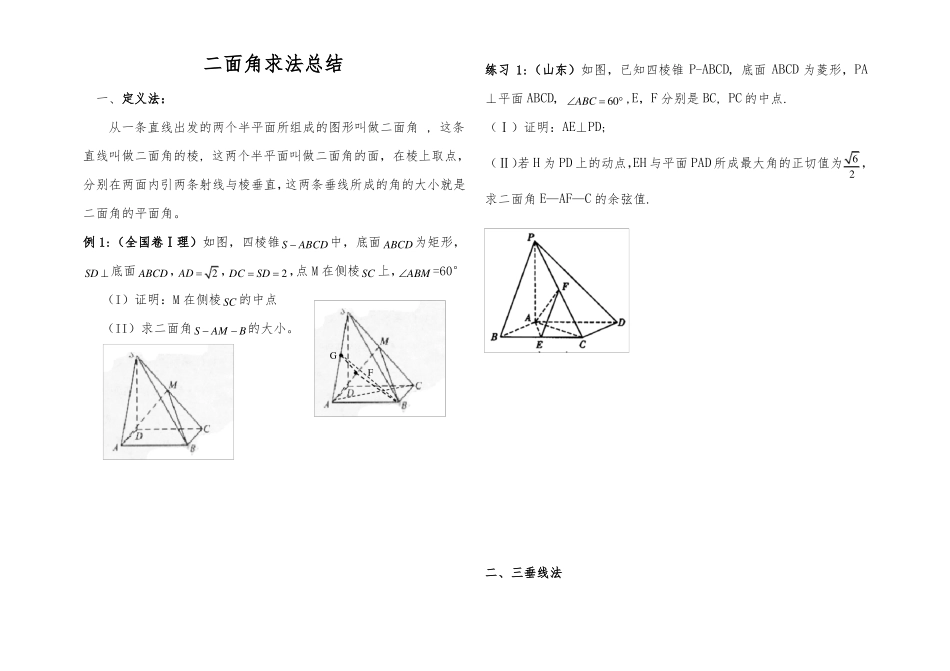
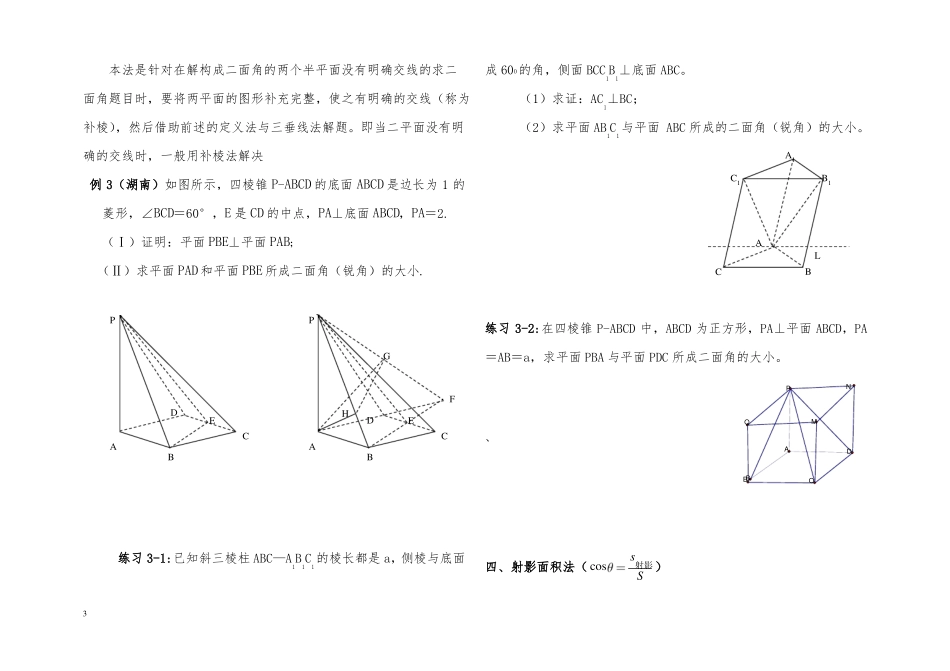
二面角求法总结一、定义法:从一条直线出发的两个半平面所组成的图形叫做二面角 , 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角。例 1:(全国卷Ⅰ理)如图,四棱锥S ABCD中,底面 ABCD为矩形,SD 底面 ABCD,AD 2 ,DC SD 2,点 M 在侧棱 SC 上,ABM =60°(I)证明:M 在侧棱 SC 的中点(II)求二面角 S AM B的大小。GF练习 1:(山东)如图,已知四棱锥 P-ABCD,底面 ABCD 为菱形,PA⊥平面 ABCD,ABC 60 ,E,F 分别是 BC, PC 的中点.(Ⅰ)证明:AE⊥PD;(Ⅱ)若 H 为 PD 上的动点,EH 与平面 PAD 所成最大角的正切值为62 ,求二面角 E—AF—C 的余弦值.二、三垂线法三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.通常当点 P 在一个半平面上则通常用三垂线定理法求二面角的大小。已知 AB 3, AD 2, PA 2, PD 2 2,PAB 60 .(Ⅰ)证明 AD 平面 PAB;(Ⅱ)求异面直线 PC 与 AD所成的角的大小;例 2.(山东卷理) 如图,在直四棱柱 ABCD-A1B1C1D1中,底面 ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA1=2, E、E1、F 分别是棱AD、AA1、AB 的中点。(1)证明:直线 EE1//平面 FCC1;(2)求二面角 B-FC1-C 的余弦值。练习 2(天津)如图,在四棱锥P ABCD中,底面 ABCD是矩形.2(Ⅲ)求二面角 P BD A的大小.三.补棱法本法是针对在解构成二面角的两个半平面没有明确交线的求二成 600的角,侧面 BCC1B1⊥底面 ABC。面角题目时,要将两平面的图形补充完整,使之有明确的交线(称为补棱),然后借助前述的定义法与三垂线法解题。即当二平面没有明确的交线时,一般用补棱法解决例 3(湖南)如图所示,四棱锥 P-ABCD 的底面 ABCD 是边长为 1 的菱形,∠BCD=60°,E 是 CD 的中点,PA⊥底面 ABCD,PA=2.(Ⅰ)证明:平面 PBE⊥平面 PAB;(Ⅱ)求平面 PAD 和平面 PBE 所成二面角(锐角)的大小.PPGFDEHDECBCAAB练习 3-1:已知斜三棱柱 ABC—A1B1C1的棱长都是 a,侧棱与底面3(1)求证:AC1⊥BC;(2)求平面 AB1C1与平面 ABC 所成的二面角(锐角)的大小。A1C1B1ALCB练习 3-2:在四棱锥 P-ABCD 中,ABCD ...