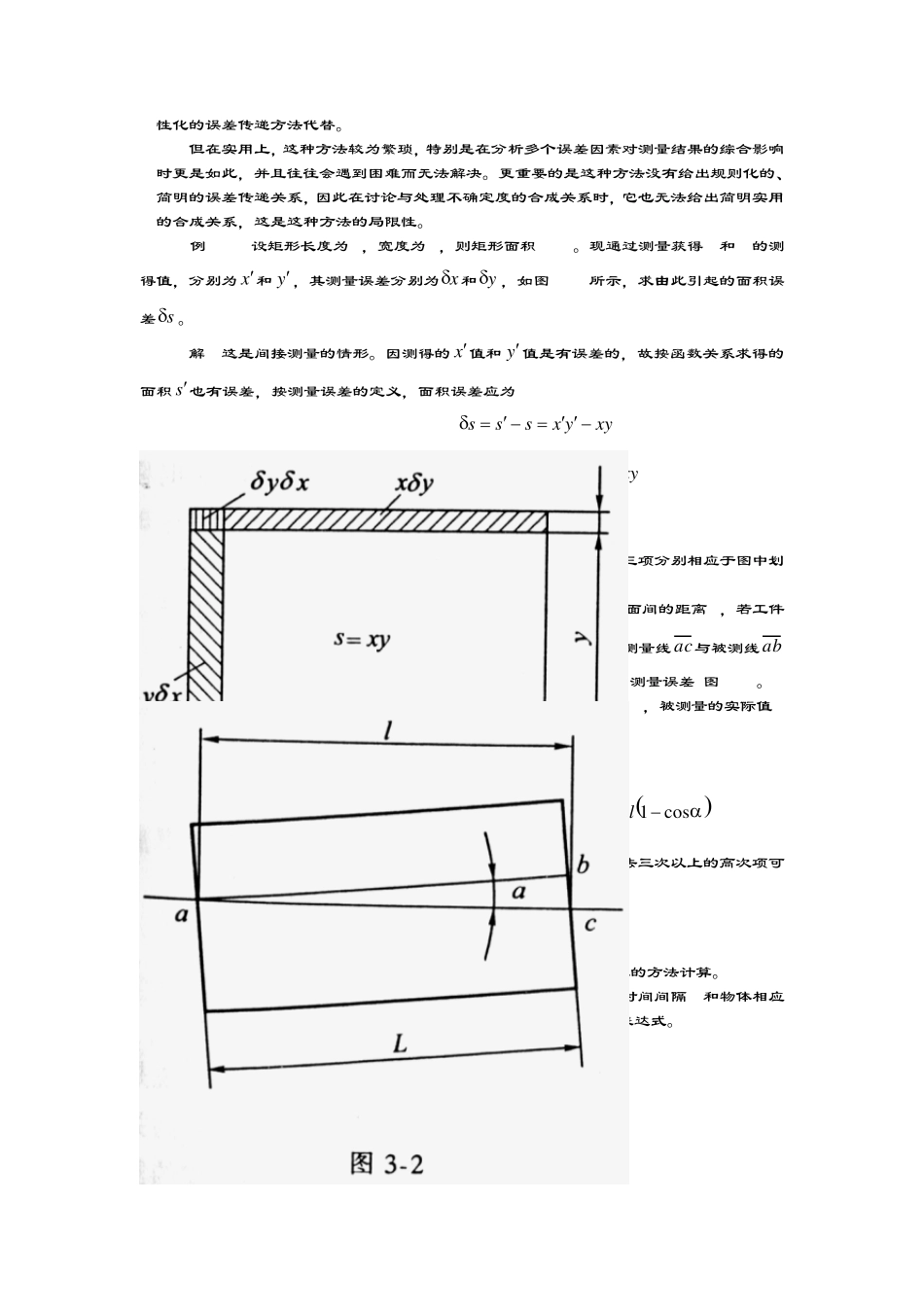
第三章 测量误差的传递 在间接测量中,待求量通过间接测量的方程式),,,(21nxxxfy获得。通过测量获得量nxxx,,,21的数值后,即可由上面的函数关系计算出待求量y的数值。那么测量数据的误差怎样作用于间接量y,即给定测量数据nxxx,,,21的测量误差,怎样求出所得间接量y的误差值? 对于更一般的情形,测量结果的误差是测量方法各环节的诸误差因素共同作用的结 果。这些误差因素通过一定的关系作用于测量结果。现研究怎样确定这一传递关系,即怎样由诸误差因素分量计算出测量的总误差。 研究测量误差的传递规律有重要意义,它不仅可直接用于已知系统误差的传递计算, 并且是建立不确定度合成规则的依据,因而是精度分析的基础①。 3.1 按定义计算测量误差 现在按测量误差的定义给出测量结果的误差,这是研究误差传递关系的基本出发点。 若对量Y用某种方法测得结果y,则按测量误差的定义,该数据的测量误差应为 Yyy (3-1) 设有如下测量方程 ),,,(21nxxxfy 式中 y——间接测量结果; nxxx,,,21——分别为各直接测得值。 直接量的测量数据nxxx,,,21的测量误差分别为 111Xxx, 222Xxx …………… nnnXxx 式中,X1,X2,…,Xn分别为相应量的实际值(真值)。 则间接测量结果的误差可写为 nnXXXfxxxfYyy,,,,,,2121 nnnXXXfxXxXxXf,,,,,,212211 (3-2) 上式给出了由测量数据的误差计算间接量y的误差的传递关系式,这一误差关系是 准确无误的。 直接按定义计算测量结果误差的方法在误差传递计算中经常使用,特别是在单独分 析某项误差因素对测量结果的影响时,若这一影响关系不便或不能化成简单的线性关系, 则这一方法更常使用。因此直接按定义作误差传递计算的方法不能完全用下面所述的线 性化的误差传递方法代替。 但在实用上,这种方法较为繁琐,特别是在分析多个误差因素对测量结果的综合影响 时更是如此,并且往往会遇到困难而无法解决。更重要的是这种方法没有给出规则化的、 简明的误差传递关系,因此在讨论与处理不确定度的合成关系时,它也无法给出简明实用 的合成关系,这是这种方法的局限性。 例 3-1 设矩形长度为x,宽度为y,则矩形面积 s=xy。现通过测量获得 x和 y的测 得值,分别为x 和 y ,其测量误差分别为x 和 y ,如图 3-1所示,求由此引起的面积误差s 。 解 这是间接测量的情形。...