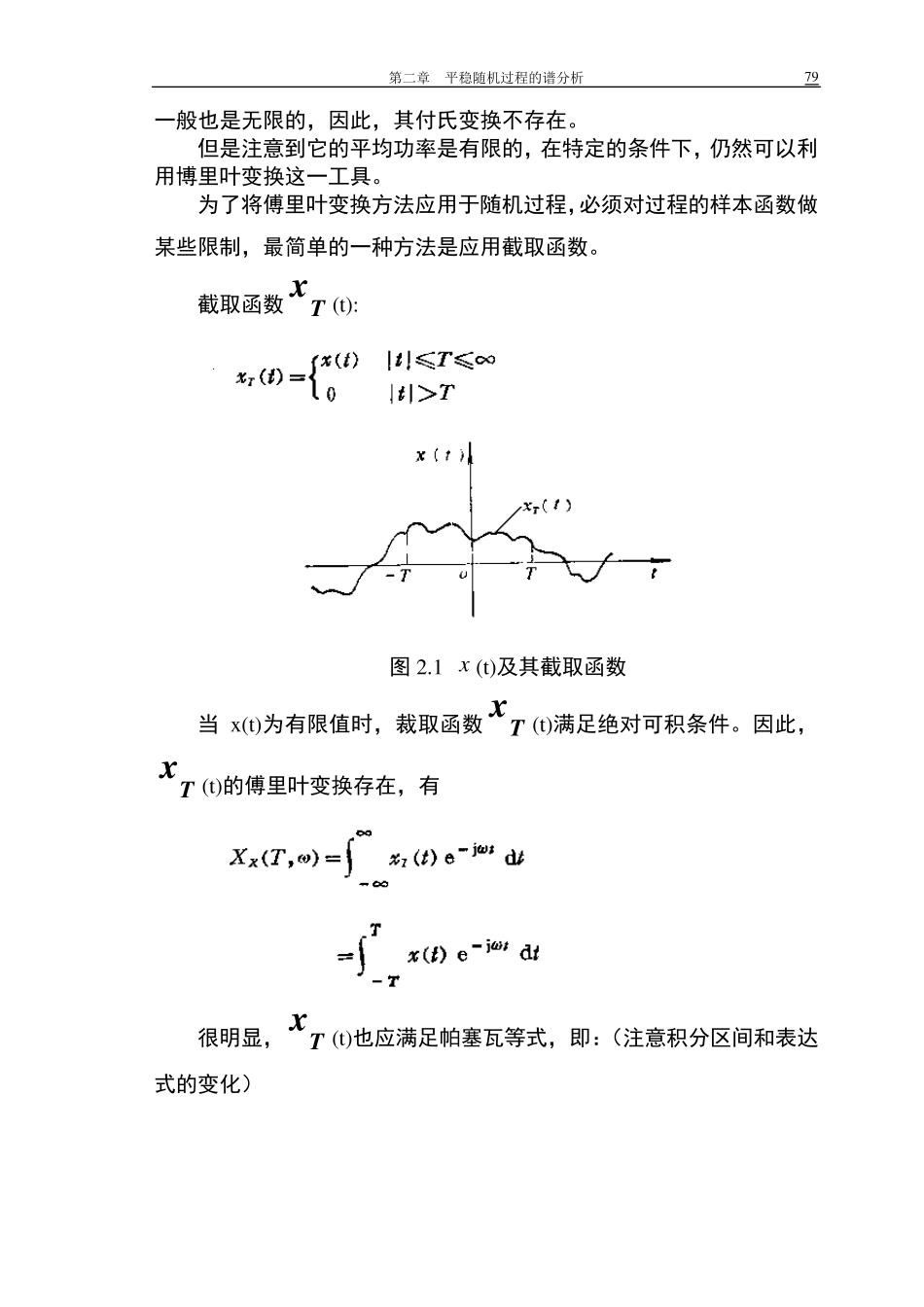
第二章 平稳随机过程的谱分析 7 7 第二章 平稳随机过程的谱分析 本章要解决的问题: ● 随机信号是否也可以应用频域分析方法? ● 傅里叶变换能否应用于随机信号? ● 相关函数与功率谱的关系 ● 功率谱的应用 ● 采样定理 ● 白噪声的定义 2 .1 随机过程的谱分析 2.1.1 预备知识 1、付氏变换: 对于一个确定性时间信号x (t),设 x (t)是时间 t 的非周期实函数,且 x (t) 满足狄利赫利条件(有限个极值,有限个断点,断点为有限值)且绝对可积,能量有限,则 x (t)傅里叶变换存在。即: 满足上述三个条件的x (t)的傅里叶变换为: 随机信号分析与应用 7 8 其反变换为: 2、帕赛瓦等式 由上面式子可以得到: ——称为非周期性时间函数的帕塞瓦(Parsev al)等式。 物理意义:若 x (t)表示的是电压(或电流),则上式左边代表 x (t)在时间(- , )区间的总能量(单位阻抗)。因此,等式右边的被积函数2)(XX 表示了信号x (t)能量按频率分布的情况,故称2)(XX为能量谱密度。 2.1.2、随机过程的功率谱密度 一个信号的付氏变换是否存在,需要满足三个条件,那么随机信号是否满足这三个条件从而存在付氏变换呢? 随机信号持续时间无限长,因此,对于非 0 的样本函数,它的能量第二章 平稳随机过程的谱分析 79 一般也是无限的,因此,其付氏变换不存在。 但是注意到它的平均功率是有限的,在特定的条件下,仍然可以利用博里叶变换这一工具。 为了将傅里叶变换方法应用于随机过程,必须对过程的样本函数做某些限制,最简单的一种方法是应用截取函数。 截取函数Tx(t): 图 2.1 x (t)及其截取函数 当 x (t)为有限值时,裁取函数Tx(t)满足绝对可积条件。因此,Tx(t)的傅里叶变换存在,有 很明显,Tx(t)也应满足帕塞瓦等式,即:(注意积分区间和表达式的变化) 随机信号分析与应用 80 用2T除上式等号的两端,可以得到 等号两边取集合平均,可以得到: 令T,再取极限,便可得到随机过程的平均功率。 交换求数学期望和积分的次序,可以得到:(注意这里由一条样本函数推广到更一般的随机过程,即下面式子对所有的样本函数均适用) dTTXEdttXETXTTTT2]),([lim21)]([21lim22 上式等号的左边表示的正是随机过程消耗在单位电阻上的平均功率(包含时间平均和统计平均),以后我们将简称它为随机过程的功率并记为 Q。再看等式的右边,它当然也存在,并...