第二章控制系统的数学模型

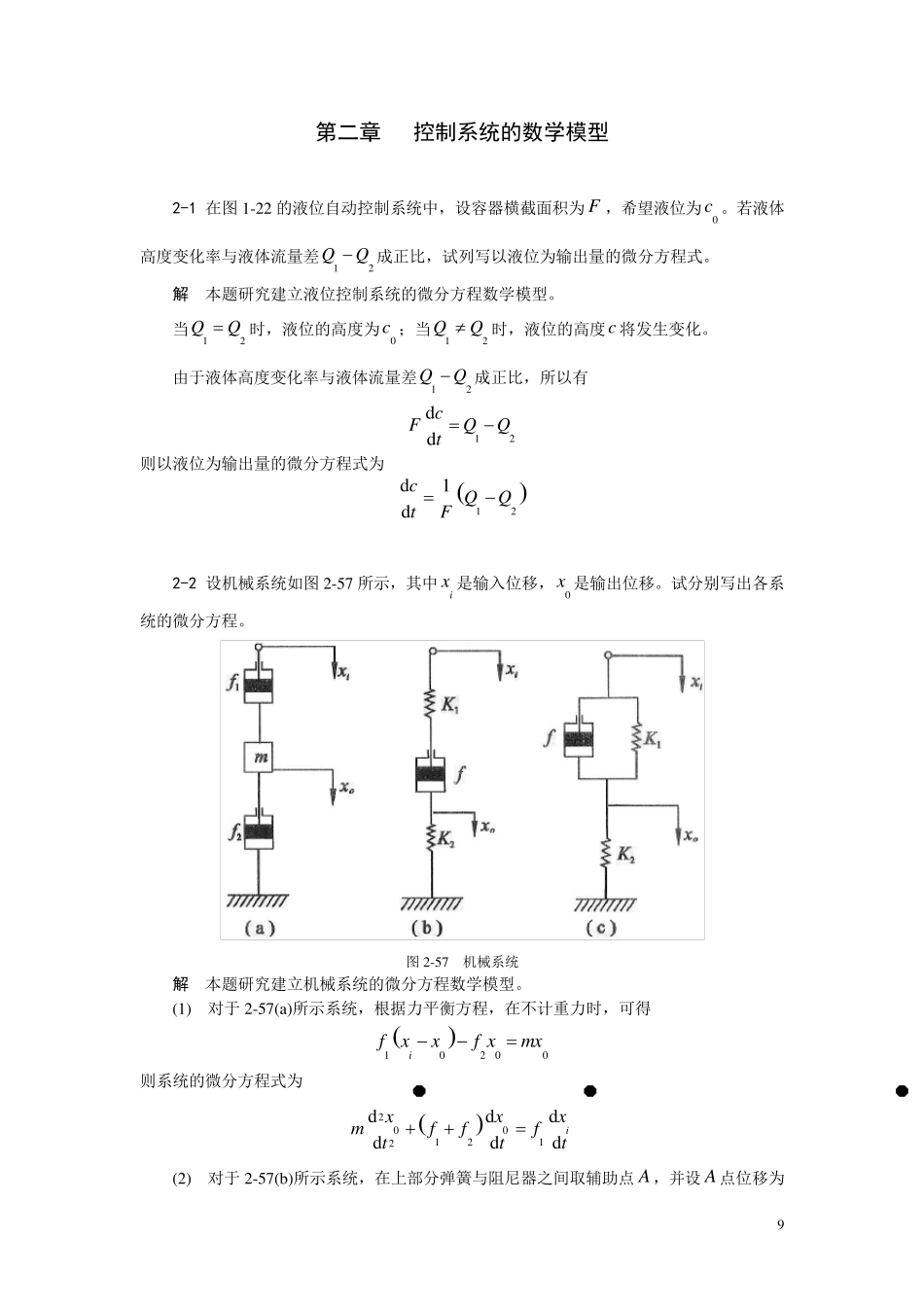
9 第二章 控制系统的数学模型 2-1 在图1-22 的液位自动控制系统中，设容器横截面积为F ，希望液位为0c 。若液体高度变化率与液体流量差12QQ成正比，试列写以液位为输出量的微分方程式。 解 本题研究建立液位控制系统的微分方程数学模型。 当12QQ时，液位的高度为0c ；当12QQ时，液位的高度c 将发生变化。 由于液体高度变化率与液体流量差12QQ成正比，所以有 12ddcFQQt  则以液位为输出量的微分方程式为 12d1dcQQtF 2-2 设机械系统如图2-57 所示，其中ix 是输入位移，0x 是输出位移。试分别写出各系统的微分方程。 图2-57 机械系统 解 本题研究建立机械系统的微分方程数学模型。 (1) 对于 2-57(a)所示系统，根据力平衡方程，在不计重力时，可得 10200ifxxf xmx 则系统的微分方程式为 2001212ddddddixxxmfffttt (2) 对于 2-57(b)所示系统，在上部分弹簧与阻尼器之间取辅助点 A ，并设A 点位移为 10 x ，方向向下。根据力平衡方程，在不计重力时，可得下列方程 10iKxxf xx 200K xf xx 消去中间变量 x ，由于 201iK xKxx， 201iKxxxK 201iKxxxK 故有 12011011020iK K xK fxK fxfK xfK xfK x 则系统的微分方程式为 0121201ddddixxf KKK K xK ftt (3) 对于 2-57(c)所示系统，根据力平衡方程，在不计重力时，可得 10020iiKxxf xxK x 则系统的微分方程式为 01201ddddiixxfKKxfK xtt 2-3 试证明图 2-58(a)的电网络与(b)的机械系统有相同的数学模型。 (a) (b) 图 2-58 电网络与机械系统 解 本题研究用拉氏变换法建立系统的传递函数数学模型。 (1) 对于图 2-58(a)，根据复数阻抗的方法可得电网络的传递函数为 11    2021122111111aiRUsC sGsUsR C sRC sRC s 2121211222121211221211R R C C sR CR CsR R C C sR CR CR Cs (2) 对于图2-58(b)，在弹簧1K 和阻尼器1f 之间引入辅助点，设其位移为x ，方向向下。根据力平衡方程，在不计重力时，可得 202010iiKxxfxxfxx 110K xfxx 对上述两式进行拉氏变换，考虑初始条件为零，可得       220220101iiK XsK XsfsXsfs...