5弹性力学习题课2课时

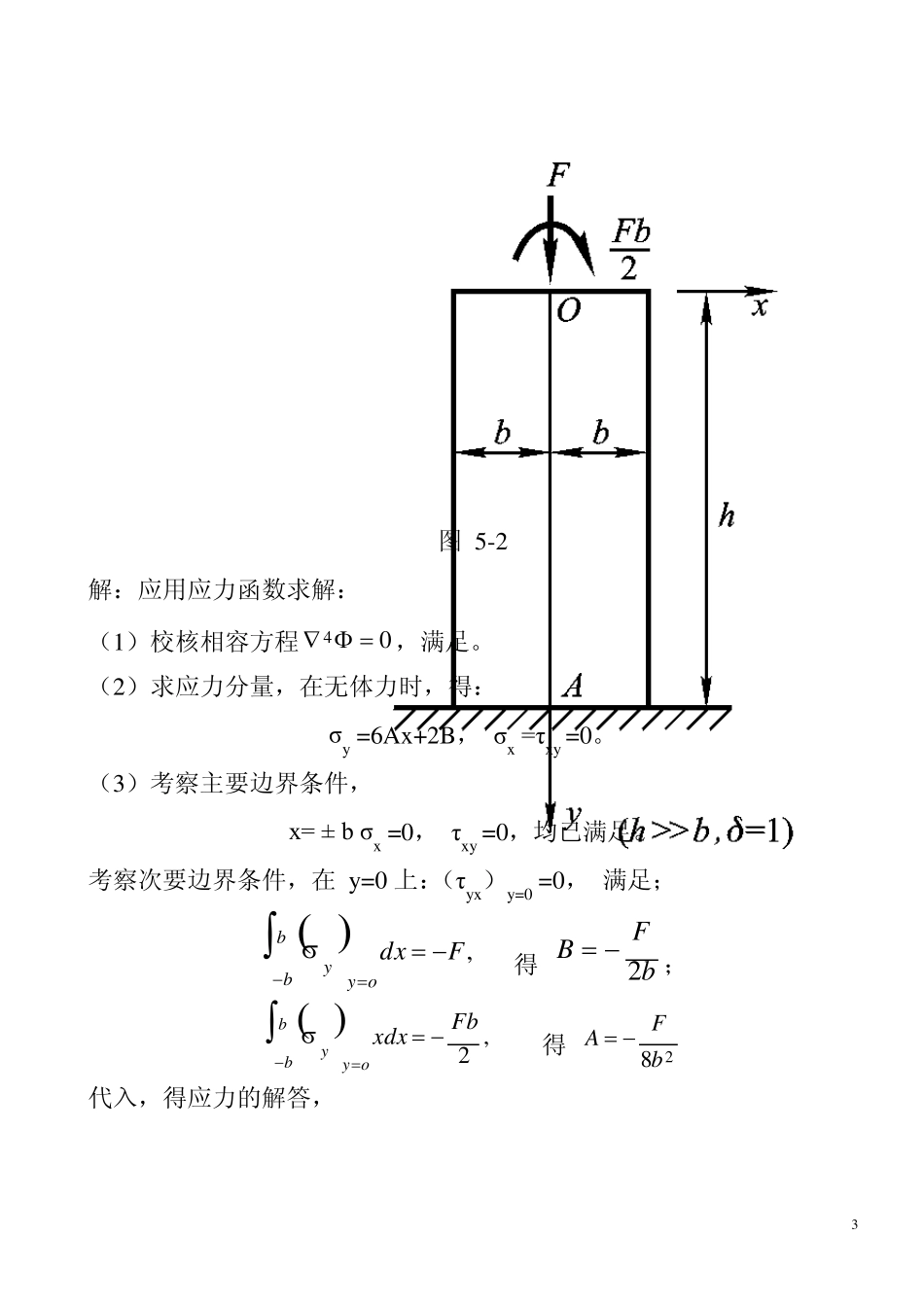
1 5 典型例题 5 .1 直角坐标解法 例题1 试列出图 5-1 的边界条件。 解：（a）对于图 5-1（a）的问题，在主要边界 y= ± h/2 应精确满足下列边界条件： 图 5- 1 2,,02yxyhxyql   1,0,2yxyhyq 在小边界（次要边界）x= 0，应用圣维南原理，列出三个积分的近似条件，当板厚 δ=1 时， 2  2/2/02/2/02/2/0111hhsxxyhhxxhhxxFdyMydyFdy 在小边界xl 处，当平衡微分方程和其他各边界条件都已满足的条件下，三个积分的边界条件必然满足，可以不必校核。 （b）在主要边界 x=0，b，应精确满足下列边界条件： x=0，σx = -ρgy，τxy =0； x= b，σx =0， τxy = - q。 在小边界 y=0，列出三个积分的边界条件，当板厚 δ=1 时：    byxybyybyyFdxFbxdxFdx00000021431231 注意，在列力矩的条件时，两边均是对原点 O 的力矩来计算的。对于 y=h的小边界可以不必校核。 例题 2 图 5-2 所示的矩形截面柱体，在顶部受有集中力 F 和力矩 M =Fb/2的作用，试用应力函数： Φ = Ax3+ Bx2 求解图示问题的应力及位移，设在 A 点的位移和转角均为零。 3 图 5-2 解：应用应力函数求解： （1）校核相容方程 04，满足。 （2）求应力分量，在无体力时，得： σy =6Ax+2B， σx =τxy =0。 （3）考察主要边界条件， x= ± b σx =0， τxy =0，均已满足。 考察次要边界条件，在 y=0 上：（τyx）y=0 =0， 满足；  ,Fdxoybby 得 bFB2；  ,2Fbxdxoybby 得 28bFA 代入，得应力的解答， 4  bxbFy2312， σx =τxy =0。 上述 Φ 和应力已满足了04和全部边界条件，因而是上述问题的解。 （4）求应变分量，  bxEbFx2312， bxEbFy2312，0xy （5）求位移分量， 由 bxEbFxux2312，对 x 积分，得：  yfbxxEbFu12232 ； 由 bxEbFyvy2312，对 y 积分，得：  xfbxyyEbFv2232 将 u，v 代入几何方程第三式 0xy...