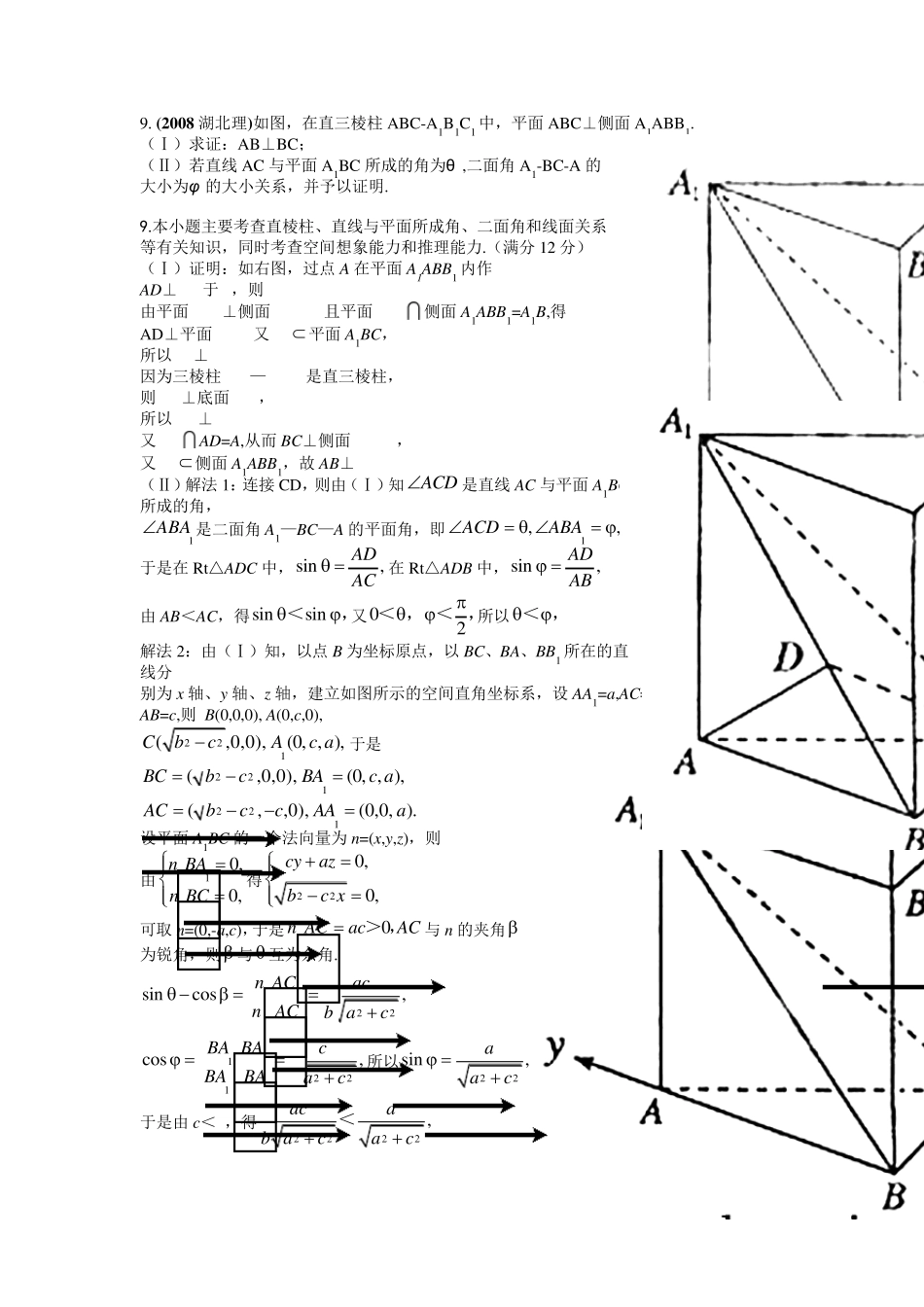
9. (2 0 0 8 湖北理)如图,在直三棱柱ABC-A1B1C1 中,平面ABC⊥侧面A1ABB1. (Ⅰ)求证:AB⊥BC; (Ⅱ)若直线AC 与平面A1BC 所成的角为θ ,二面角A1-BC-A 的大小为φ 的大小关系,并予以证明. 9.本小题主要考查直棱柱、直线与平面所成角、二面角和线面关系等有关知识,同时考查空间想象能力和推理能力.(满分12 分) (Ⅰ)证明:如右图,过点A 在平面A1ABB1 内作 AD⊥A1B于D,则 由平面A1BC⊥侧面A1ABB1,且平面A1BC侧面A1ABB1=A1B,得 AD⊥平面A1BC,又BC 平面A1BC, 所以AD⊥BC. 因为三棱柱ABC—A1B1C1是直三棱柱, 则AA1⊥底面ABC, 所以AA1⊥BC. 又AA1AD=A,从而 BC⊥侧面A1ABB1, 又AB 侧面A1ABB1,故 AB⊥BC. (Ⅱ)解法 1:连接 CD,则由(Ⅰ)知ACD是直线AC 与平面A1BC所成的角, 1ABA是二面角A1—BC—A 的平面角,即1,,ACDABA 于是在Rt△ADC 中,sin,ADAC 在Rt△ADB 中,sin,ADAB 由AB<AC,得sinsin<,又02< ,< ,所以< , 解法 2:由(Ⅰ)知,以点B 为坐标原点,以BC、BA、BB1 所在的直线分 别为x 轴、y 轴、z 轴,建立如图所示的空间直角坐标系,设 AA1=a,AC=b, AB=c,则 B(0,0,0), A(0,c,0), 221(,0,0),(0, , ),CbcAc a于是 221(,0,0),(0, , ),BCbcBAc a 221(,,0),(0,0, ).ACbccAAa 设平面A1BC 的一个法向量为n=(x,y,z),则 由10,0,n BAn BC得220,0,cyazbc x 可取 n=(0,-a,c),于是0n ACacAC> ,与n 的夹角为锐角,则 与 互为余角. 22sincos,n ACacn ACb ac 1221cos,BA BAcBABAac 所以22sin,aac 于是由c<b,得2222,acab acac< 即sinsin ,<又0,2<,<所以,< 10. (2 0 0 8 湖南理)如图所示,四棱锥P-ABCD 的底面ABCD 是边长为1 的菱形,∠BCD=60°, E 是CD 的中点,PA⊥底面ABCD,PA=2. (Ⅰ)证明:平面PBE⊥平面PAB; (Ⅱ)求平面PAD 和平面PBE 所成二面角(锐角)的大小. 10.解: 解法一 (Ⅰ)如图所示,连结 BD,由 ABCD 是菱形且∠BCD=60°知, △BCD 是等边三角形.因为E 是CD 的中点,所以BE⊥CD,又AB∥CD, 所以BE⊥AB.又因为PA⊥平面ABCD,BE 平面ABCD,所以 PA⊥BE.而 PA AB=A,因此 BE⊥平面PAB. 又BE ...