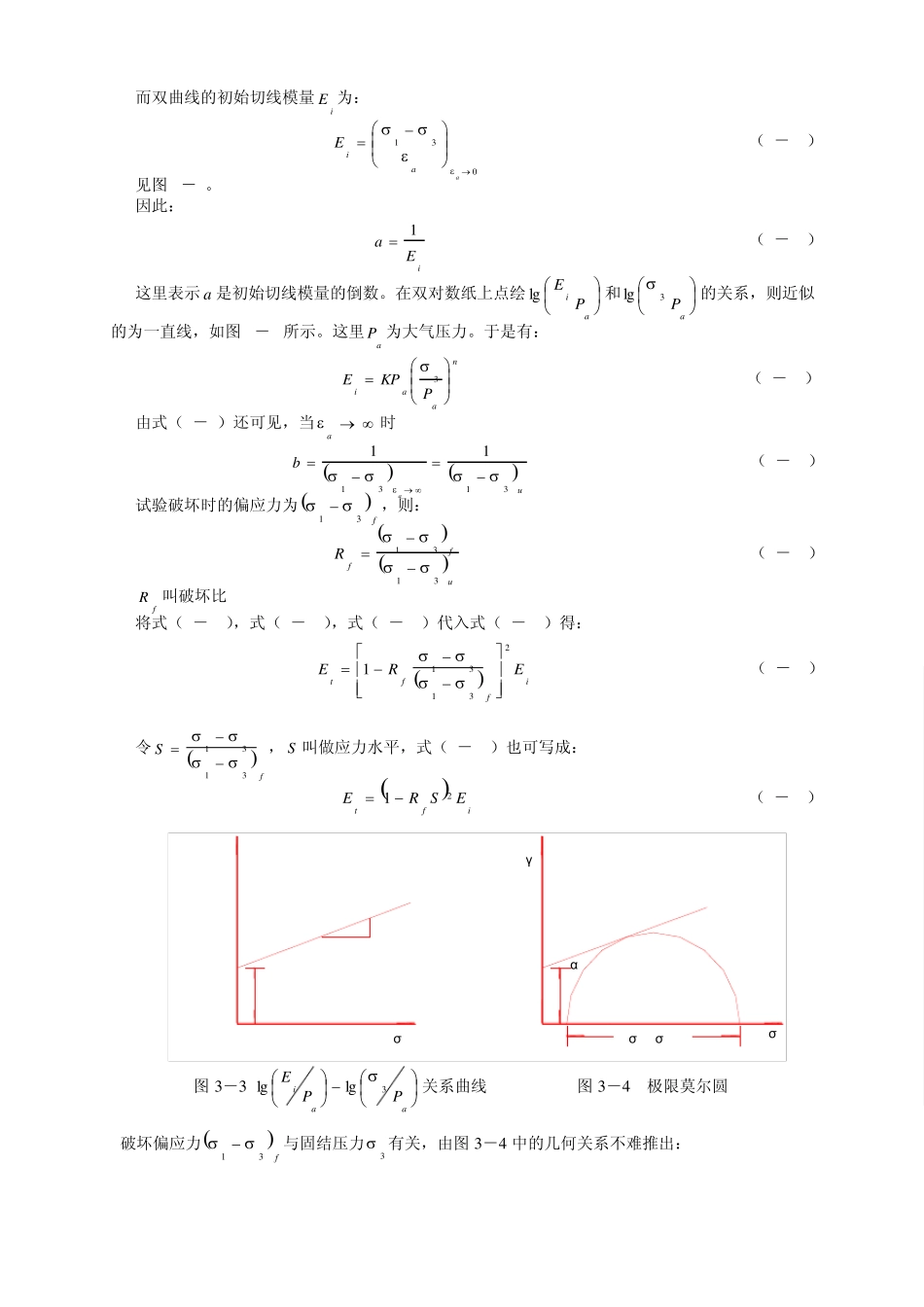
第三章 土的模型和接触面单元 3.1引入地基土非线性模型的重要性 土与结构的共同作用问题是一个无穷维的超静定问题,即使是弹性地基上的梁板问题已形成浩瀚的文献,构成了该领域中最经典的课题[1,2,3,4,5]。由于计算机和计算技术的飞跃发展,特别是大 型子结构分析方法的进展[6,7],才使得建筑结构与筏基(箱基)和地基的共同作用分析成为可能[8]。国内外建筑物的风起云涌和丰富的工程经验极大的推动了该领域的研究,取得了许多理论和应用成果[9,10]。研究成果直接应用于建筑工程实践的最大困难在于地基模型简单的取为线性模型,使得基底反力分布与实测相差甚远。分析表明,对于上部结构和与基础结构刚度都很大的情况,共同作用的关键是引入地基土的非线性模型。文献[3]给出基础板(分别取柔性板和刚性板两种情况下)地基土分别取为线性和非线性模型时四种不同组合的结果,见图1。 图中曲线 1:板、地基土均为线性模型;曲线 2:板为非线性,地基土为线性;曲线 3:板为线性,地基土为非线性;曲线 4:板、地基土均为非线性。结果表明,对柔性基础特别是混凝土铺面,应首先考虑钢筋混凝土结构的非线性,地基土取为弹性影响不大;但对于刚度大的结构,例如高层建筑结构,共同作用的当务之急是引入地基土的非线性,即考虑地基土的非线性状是分析结构物和筏基(箱基)和地基共同作用的关键问题。 文献[11]考虑了上海粉砂土地基和高层箱形基础共同作用的分析实例,地基土采用 Lade-Ducan弹塑性模型,并与弹性半空间地基模型结果作了对比,两者反力分布发生了实质性变化,显然非线性地基边、角部位的反力集中现象大为缓和,与实测统计的反力系数较接近。如果地基土按线性模型则反力远远偏离于实测结果,共同作用的分析结果难以实用。因此,引入地基土的非线性是考虑共同作用分析的关键。 3.2 本文计算程序中所采用的非线性地基土模型 常用的非线性弹性模型有两类:第一类是以 E(弹性模量)和 ν(泊松比)两个弹性常数表达的称作 E-ν 非线性弹性模型,这类模型以 Duncan-Chang 模型为代表。第二类是以 K(体积表形模量)和 G(剪切模量)两个弹性常数表达的称为 K-G 非线性弹性模型,它以 Domaschuk 模型为代表。 3.2.1邓肯曲线的 Et和 Vt模型 3.2.1.1 切线弹性模量 点绘a~31 曲线,如图3-1 所示,Kondner 等人发现,可以用双曲线来拟和这些曲线。对某一3 ,a~31 关系可表示成: aab...