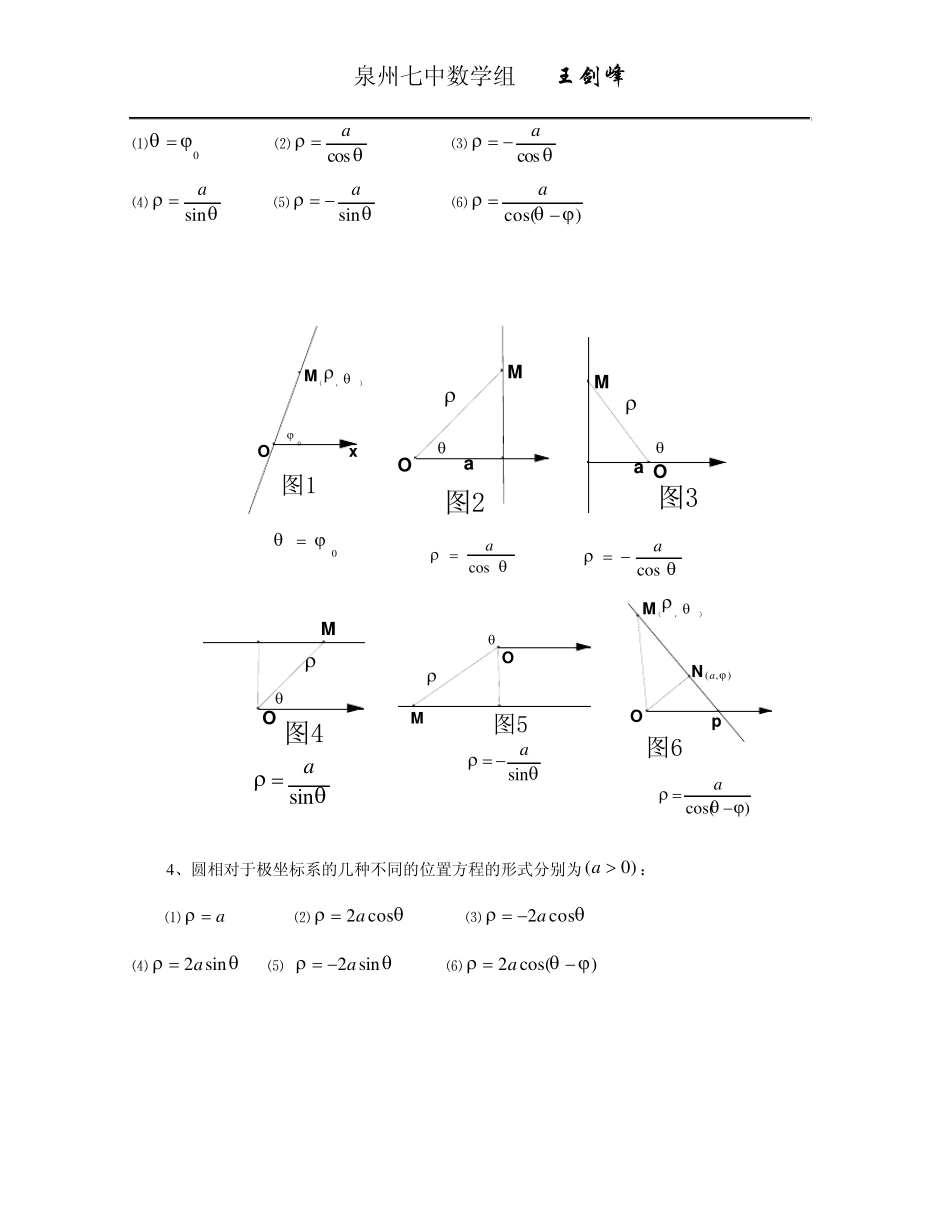
泉州七中数学组 王剑峰 J 3 参数方程和极坐标系 一、 知识要点 (一)曲线的参数方程的定义: 在取定的坐标系中,如果曲线上任意一点的坐标x 、y 都是某个变数t 的函数,即 )()(tfytfx 并且对于t 每一个允许值,由方程组所确定的点M(x ,y )都在这条曲线上,那么方程组就叫做这条曲线的参数方程,联系x 、y 之间关系的变数叫做参变数,简称参数. (二)常见曲线的参数方程如下: 1.过定点(x 0,y 0),倾角为α 的直线: sincos00tyytxx (t 为参数) 其中参数t 是以定点P(x 0,y 0)为起点,对应于t 点M(x ,y )为终点的有向线段PM 的数量,又称为点P 与点M 间的有向距离. 根据t 的几何意义,有以下结论. ○1 .设 A、B 是直线上任意两点,它们对应的参数分别为tA 和tB,则 AB =ABtt =BAABtttt4)(2. ○2 .线段AB 的中点所对应的参数值等于2BAtt. 2.中心在(x 0,y 0),半径等于r 的圆: sincos00ryyrxx ( 为参数) 3.中心在原点,焦点在x 轴(或 y 轴)上的椭圆: sincosbyax ( 为参数) (或 sincosaybx) 中心 在点(x0,y0 )焦 点在平 行 于x轴 的直线上的椭 圆 的参数方程为参数) (.sin,cos00byyaxx 4.中心在原点,焦点在x 轴(或 y 轴)上的双曲线: 泉州七中数学组 王剑峰 tgsecbyax ( 为参数) (或 ecaybxstg) 5.顶点在原点,焦点在 x 轴正半轴上的抛物线: ptyptx222 (t 为参数,p>0) 直线的参数方程和参数的几何意义 过定点 P(x 0,y 0),倾斜角为 的直线的参数方程是 sincos00tyytxx (t 为参数). J3.2 极坐标系 1、定义:在平面内取一个定点 O,叫做极点,引一条射线 Ox,叫做极轴,再选一个长度单位和角度的正方向(通常取逆时针方向)。对于平面内的任意一点 M,用ρ 表示线段 OM的长度,θ 表示从 Ox到 OM的角,ρ 叫做点 M的极径,θ 叫做点 M的极角,有序数对(ρ , θ )就叫做点 M的极坐标。这样建立的坐标系叫做极坐标系。 2、极坐标有四个要素:①极点;②极轴;③长度单位;④角度单位及它的方向.极坐标与直角坐标都是一对有序实数确定平面上一个点,在极坐标系下,一对有序实数 、 对应惟一点 P( , ),但...