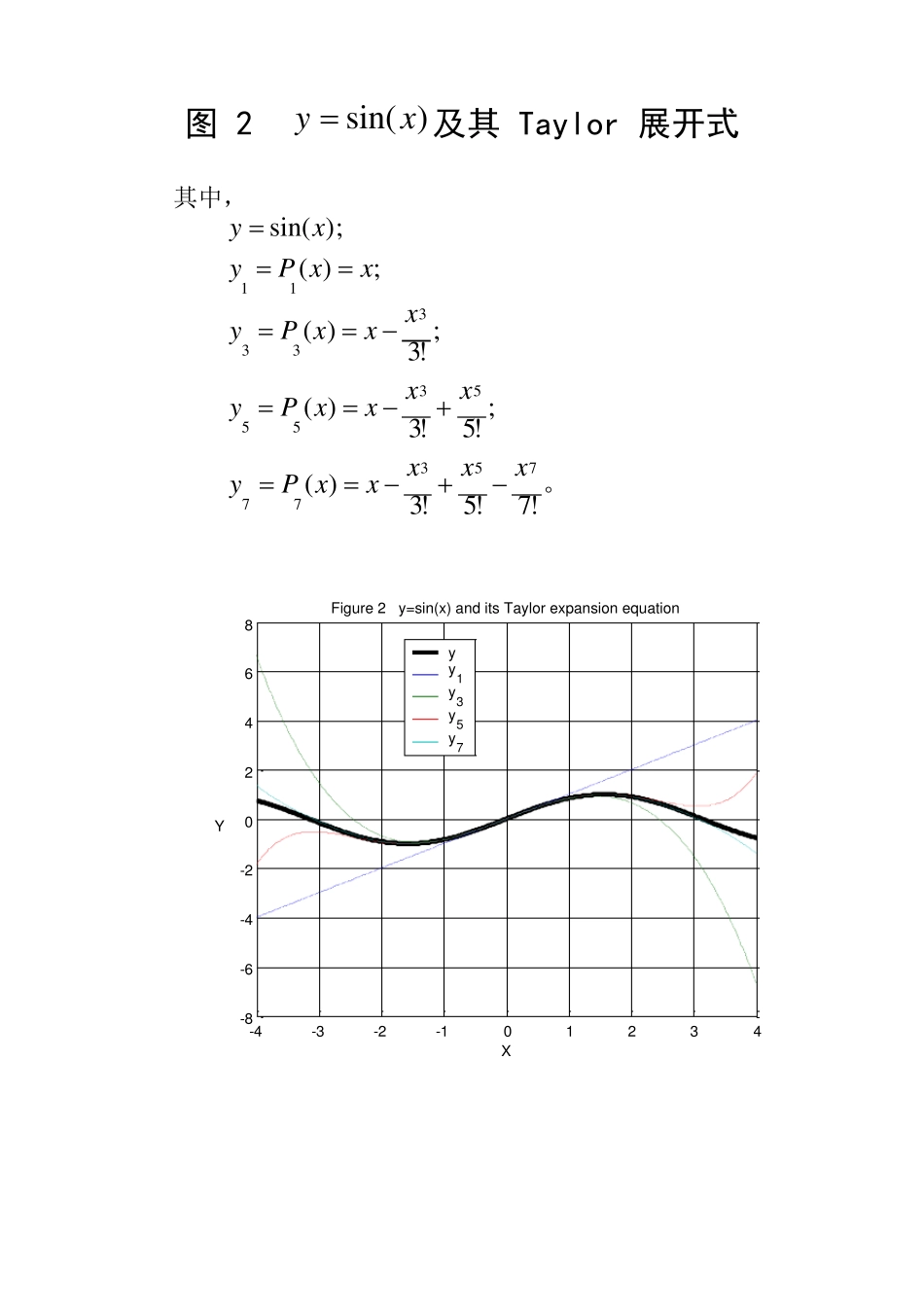
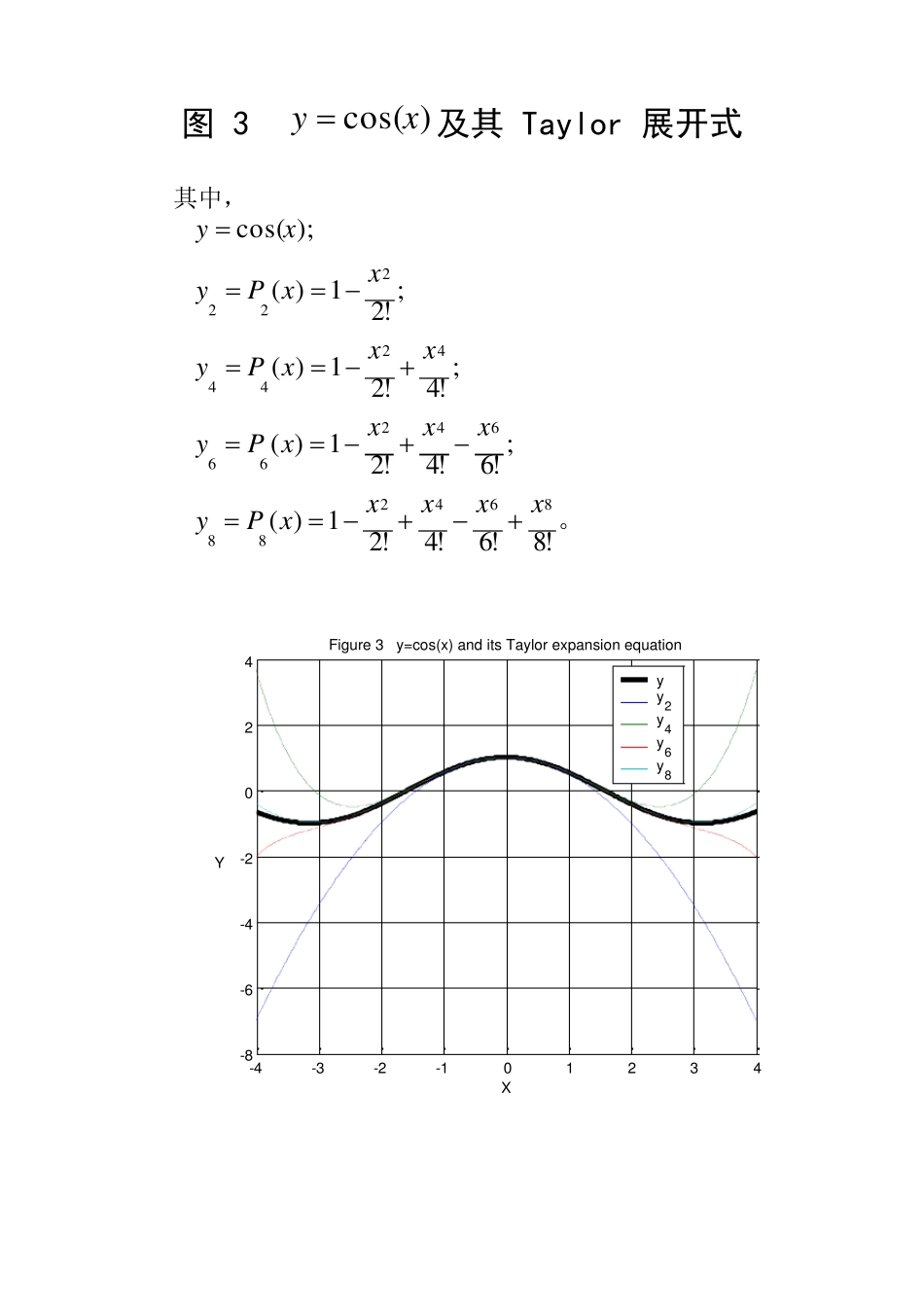
图 1 )exp(xy及其 Taylor 展开式 其中, 。!4!3!21)(;!3!21)(;!21)(;1)(;)exp(43244323322211xxxxxPyxxxxPyxxxPyxxPyexyx -3-2-10123-50510152025Figure 1 y=exp(x) and its Taylor expansion equationXYyy1y2y3y4 图 2 )sin(xy及其 Taylor 展开式 其中, 。!7!5!3)(;!5!3)(;!3)(;)();sin(75377535533311xxxxxPyxxxxPyxxxPyxxPyxy -4-3-2-101234-8-6-4-202468Figure 2 y=sin(x) and its Taylor expansion equationXYyy1y3y5y7 图 3 )cos(xy及其 Taylor 展开式 其中, 。!8!6!4!21)(;!6!4!21)(;!4!21)(;!21)();cos(864288642664244222xxxxxPyxxxxPyxxxPyxxPyxy -4-3-2-101234-8-6-4-2024Figure 3 y=cos(x) and its Taylor expansion equationXYyy2y4y6y8 图 4 )1ln (xy及其 Taylor 展开式 其中, 。432)(;32)(;2)(;)();1ln (43244323322211xxxxxPyxxxxPyxxxPyxxPyxy -1-0.500.511.52-3-2-10123Figure 4 y=ln(x) and its Taylor expansion equationXYyy1y2y3y4 图 5 )sh(xy及其 Taylor 展开式 其中, 。!7!5!3)(;!5!3)(;!3)(;)(;2)sh(75377535533311xxxxxPyxxxxPyxxxPyxxPyeexyxx -5-4-3-2-1012345-80-60-40-20020406080Figure 5 y=sh(x) and its Taylor expansion equationXYyy1y3y5y7 图 6 )ch(xy及其 Taylor 展开式 其中, 。!8!6!4!21)(;!6!4!21)(;!4!21)(;!21)(;2)ch(864288642664244222xxxxxPyxxxxPyxxxPyxxPyeexyxx -5-4-3-2-101234501020304050607080Figure 6 y=ch(x) and its Taylor expansion equationXYyy2y4y6y8 图 7 )1(xy及其 Taylor 展开式 其中, 。43244323322211!4)3)(2)(1( !3)2)(1(!2)1(1)(;!3)2)(1(!2)1(1)(;!2)1(1)(;1)(;)1(xxxxxPyxxxxPyxxxPyxxPyxy -1-0.8-0.6-0.4-0.200.20.40.60.81-2024681012141618Figure 7.1 y=(1+x)a and its Taylor expansion equation ( a = -1.5 )XYyy1y2y3y4 -1-0.8-0.6-0.4-0.200.20.40.60.810.20.40.60.811.21.41.6Figure 7.2 y=(1+x)a and its Taylor expansion equation ( a = 0.5 )XYyy1y2y3y4 -1-0.8-0.6-0.4-0.200.20.40.60.81-1001020304050Figure 7.3 y=(1+x)a and its Taylor expansion equation ( a = 5.5 )XYyy1y2y3y4