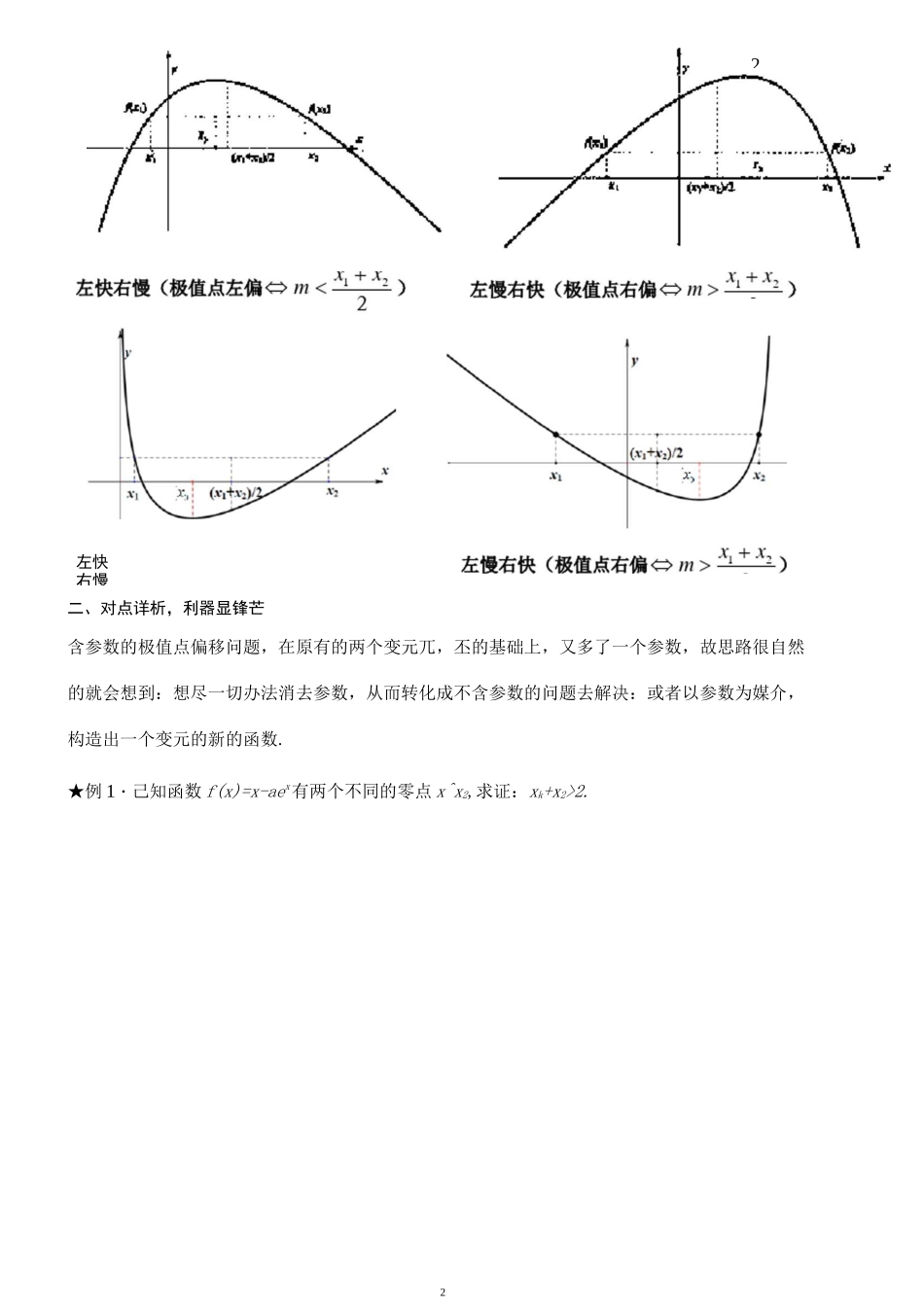
1含参数极值点偏移问题III适用区域丨人教版丨课时时长(分钟)!120!适用学科 I高中数学|适用年级|高三|1111 教学目标丨掌握含参数极值点偏移问题 III11教学重点 I掌握含参数极值点偏移问题 III4-4教学难点 I掌握含参数极值点偏移问题 I■MMWW一、极值点偏移对于可导函数 y=f(x),在区间(a,b)上只有一个极大(小)值点儿,方程/(x)=0 的解分别为 XL,X2,且 a
)x°,即函数 y=/(x)在区间 3,七)上乙极(小)大值点心右(左)偏:⑵ 若几兀)>/(2 兀—耳),则送±>(v)x°,即函数 y=f(x)在区间(兀,兀)上极(小)大值点兀右(左)偏.证明:(1)因为对于可导函数 y=/(X),在区间(。上)上只有一个极大(小)值点忑,则函数/(x)的单调递增(减)区间为(a,x°),单调递减(增)区间为(x°,b),由于a)2x0-x2,所以肯殳<(>)兀,即函数极(小)大值点 X。右(左)偏;(2)证明略.2二、对点详析,利器显锋芒含参数的极值点偏移问题,在原有的两个变元兀,丕的基础上,又多了一个参数,故思路很自然的就会想到:想尽一切办法消去参数,从而转化成不含参数的问题去解决:或者以参数为媒介,构造出一个变元的新的函数.★例 1・己知函数 f(x)=x-aex有两个不同的零点 x^x2,求证:xk+x2>2.左快右慢23★例 2.已知函数/(x)=iiix-ox-,d 为常数,若函数/(x)有两个零点,证明:x^x2>e2.★例 3•已知心兀是函数 f(x)=ex-ax 的两个零点,且兀2;(2)求证:x^x2<1.5★例 4•已知 1 函数 f(x)=x-ea\a>0),若存在0),函数广(x)为 f(x)的导函数,且 XA(xlJ(xi)),B(x2J(x2))是/(x)的图像上不同的两点,满足/(xj+/(x2)=0,线段 4〃中点的横坐标为证明:0¥。>1・9★已知函数/(x)=a---]nx(aeR).x(1)若 d=2,求函数/(x)在(1,K)上的零点个数;(2)若/(x)有两零点(兀<吃),求证:2<呂+兀<3/1...